题目内容
10.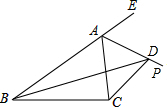 如图,D是△ABC的外角∠CAE平分线AP上一点,求证:DC+DB>AB+AC.
如图,D是△ABC的外角∠CAE平分线AP上一点,求证:DC+DB>AB+AC.
分析 在AE上截取AH=AC,连接DH,由AD平分∠CAE,得到一对角相等,利用SAS得到△ADH≌△ACD,利用全等三角形对应边相等得到DC=DH,在三角形BHD中,根据三边关系得到BD+HD>BH,等量代换即可得证.
解答 证明:在AE上截取AH=AC,连接DH,如图所示:
∵AD平分∠CAE,
∴∠DAH=∠CAD,
在△ADH和△ADC中,
$\left\{\begin{array}{l}{AH=AC}\\{∠DAH=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△ADH≌△ADC(SAS),
∴CD=HD,
在△BHD中,BD+HD>BH=AB+AH=AB+AC,
∴DC+DB>AB+AC.
点评 此题考查了全等三角形的判定与性质,三角形的三边关系,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
20.下列一元二次方程中,没有实数根的是( )
| A. | x2-2x-1=0 | B. | x2-2x+1=0 | C. | x2-1=0 | D. | x2+2x+3=0 |

 已知:如图,AB⊥BC,AE⊥ED,AB=AE,∠ACD=∠ADC,求证:BC=ED.
已知:如图,AB⊥BC,AE⊥ED,AB=AE,∠ACD=∠ADC,求证:BC=ED.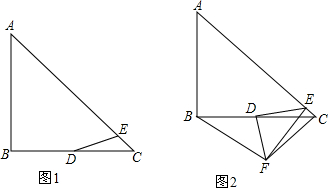
 A,B两地间的铁路线长828km,如图是一列慢车和一列快车沿相同路线从A地到B地所行驶的路程y(km)和行驶时间x(h)的变化的图象,根据图象回答下列问题:
A,B两地间的铁路线长828km,如图是一列慢车和一列快车沿相同路线从A地到B地所行驶的路程y(km)和行驶时间x(h)的变化的图象,根据图象回答下列问题: