Question

1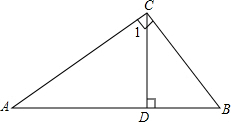．如图所示，在△ACB中，∠ACB=90°，∠1=∠B．
（1）求证：CD⊥AB；
（2）如果AC=8，BC=6，AB=10，求CD的长．

Answer 1

分析 （1）先由∠ACB=90°，得出∠1+∠BCD=90°，而∠1=∠B，等量代换得到∠B+∠BCD=90°，再根据三角形内角和定理求出∠BDC=90°，根据垂直的定义即可证明CD⊥AB；
（2）根据三角形的面积公式可得S_△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC，那么CD=$\frac{AC•BC}{AB}$，将数值代入计算即可求解．

解答 （1）证明：∵∠ACB=90°，
∴∠1+∠BCD=90°，
∵∠1=∠B，
∴∠B+∠BCD=90°，
∴∠BDC=90°，
∴CD⊥AB；

（2）解：∵S_△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC，
∴CD=$\frac{AC•BC}{AB}$=$\frac{8×6}{10}$=4.8．

点评 本题考查了直角三角形的性质，三角形内角和定理，垂直的定义，三角形的面积，比较简单．求出∠BDC=90°是解题的关键．