题目内容
10．抛物线y=-x2+3x+h的顶点的纵坐标是k，则k-h的值是$\frac{9}{4}$．分析 先根据顶点公式求得k，再求k-h的值即可．
解答 解：抛物线y=-x2+3x+h的顶点的纵坐标k=$\frac{4ac-{b}^{2}}{4a}$=$\frac{-4h-9}{-4}$，
∴k-h=$\frac{-4h-9}{-4}$-h=$\frac{-4h-9+4h}{-4}$=$\frac{9}{4}$，
故答案为$\frac{9}{4}$．
点评 本题考查了二次函数的性质，熟记抛物线的顶点坐标（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$）是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
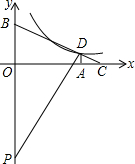如图，在平面直角坐标系中，Rt△PBD的斜边PB落在y轴上，tan∠BPD=$\frac{1}{2}$．延长BD交x轴于点C，过点D作DA⊥x轴，垂足为A，PD与x轴交于点E，OA=8，OB=6．
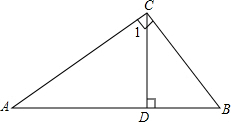如图所示，在△ACB中，∠ACB=90°，∠1=∠B．
9．
如图，⊙O是△ABC的外接圆，AB是⊙O的直径，I为△ABC的内心，AI的延长线交BC于D，若OI⊥AD，则tan∠CAD的值为（ ）
如图，⊙O是△ABC的外接圆，AB是⊙O的直径，I为△ABC的内心，AI的延长线交BC于D，若OI⊥AD，则tan∠CAD的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{\sqrt{5}}{2}$ |
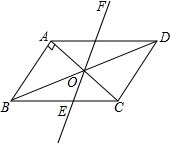如图，?ABCD中，AB⊥AC，AB=1，BC=$\sqrt{5}$．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F．
7．
如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）
如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）| A． | $\sqrt{8}$ | B． | 3 | C． | 4 | D． | $\sqrt{32}$ |