题目内容
12.已知二次函数y=x2-2x+4,若过原点O的直线与该二次函数的图象只有一个公共点,则这样的直线有3条.分析 应该有三条,设直线的解析式为y=kx,则与二次函数联立可以得到两个解,这是两条,还有一条就是x=0.
解答 解:设直线的解析式为y=kx,
则$\left\{\begin{array}{l}{y=kx}\\{y={x}^{2}-2x+4}\end{array}\right.$,
消去y得x2-(k+2)x+4=0,
∵过原点O的直线与该二次函数的图象只有一个公共点,
∴(k-2)2-16=0,
∴k=6或-2,
∴直线为y=6x或y=-2x,
当过原点的直线与对称轴平行时也只有一个交点,则直线x=0,
∴这样的直线有3条.
故答案为3.
点评 本题考查了二次函数的性质以及直线与抛物线的交点问题的应用,解题关键是联立列方程组.

练习册系列答案
相关题目
2.计算$\frac{x-1}{x}$+$\frac{1}{x}$=( )
| A. | 1 | B. | $\frac{1}{x}$ | C. | $\frac{x+1}{x}$ | D. | $\frac{x-1}{x}$ |
17.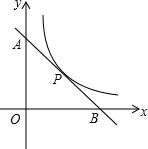 如图,一次函数y=-2x+4的图象与坐标轴分别交于A、B两点,点P在直线AB上运动(点P不与A,B两点重合),反比例函数y=$\frac{k}{x}$过点P,求k的最大值( )
如图,一次函数y=-2x+4的图象与坐标轴分别交于A、B两点,点P在直线AB上运动(点P不与A,B两点重合),反比例函数y=$\frac{k}{x}$过点P,求k的最大值( )
 如图,一次函数y=-2x+4的图象与坐标轴分别交于A、B两点,点P在直线AB上运动(点P不与A,B两点重合),反比例函数y=$\frac{k}{x}$过点P,求k的最大值( )
如图,一次函数y=-2x+4的图象与坐标轴分别交于A、B两点,点P在直线AB上运动(点P不与A,B两点重合),反比例函数y=$\frac{k}{x}$过点P,求k的最大值( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
4.将1:10000的某幅地图,表示范围不变,图幅放大为原来的4倍,新地图的比例尺为( )
| A. | 五千分之一 | B. | 图上一厘米代表实地距离5000米 | ||
| C. | 1:1000 | D. | $\frac{1}{20000}$ |
9. 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则tan∠CAD的值为( )
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则tan∠CAD的值为( )
 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则tan∠CAD的值为( )
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则tan∠CAD的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
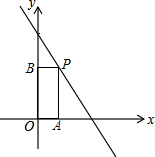 (1)如图,在一次函数y=-x+3的图象上取点P,作PA⊥x轴,作PB⊥y轴,垂足分别为A,B,且矩形OAPB的面积为2,则这样的点有A;
(1)如图,在一次函数y=-x+3的图象上取点P,作PA⊥x轴,作PB⊥y轴,垂足分别为A,B,且矩形OAPB的面积为2,则这样的点有A;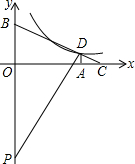 如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=$\frac{1}{2}$.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,PD与x轴交于点E,OA=8,OB=6.
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=$\frac{1}{2}$.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,PD与x轴交于点E,OA=8,OB=6.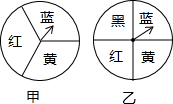 如图,有甲、乙两个转盘,每个转盘上各个扇形的圆心角都相等,让两个转盘分别自由转动一次,当转盘指针落在分界线上时,重新转动.
如图,有甲、乙两个转盘,每个转盘上各个扇形的圆心角都相等,让两个转盘分别自由转动一次,当转盘指针落在分界线上时,重新转动.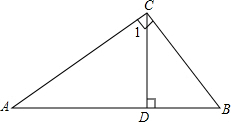 如图所示,在△ACB中,∠ACB=90°,∠1=∠B.
如图所示,在△ACB中,∠ACB=90°,∠1=∠B.