题目内容
9. 如图,在△ABC中,BC=2AC,∠C=2∠B,求证:∠A=90°.
如图,在△ABC中,BC=2AC,∠C=2∠B,求证:∠A=90°.
分析 作∠ACB的平分线CD交AB于点D,过D作DE⊥BC于点E,构造直角三角形和等腰三角形,由∠ACD=∠BCD,∠C=2∠B得到∠BCD=∠B⇒△DBC是等腰三角形,由SAS证得△ECD≌△ACD,从而得到结论.
解答  证明:作∠ACB的平分线CD交AB于点D,过D作DE⊥BC于点E,
证明:作∠ACB的平分线CD交AB于点D,过D作DE⊥BC于点E,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∵∠C=2∠B,
∴∠BCD=∠B,
∴△DBC是等腰三角形,
又∵DE⊥BC,
∴CE=$\frac{1}{2}$BC.
∵BC=2AC,
∴CE=CA,
在△BED与△BCD中,
$\left\{\begin{array}{l}{CE=CA}\\{∠ACD=∠BCD}\\{CD=CD}\end{array}\right.$,
∴△BED≌△BCD(SAS).
∴∠A=∠CED=90°.
点评 本题考查了等腰三角形的判定和性质及直角三角形全等三角形的判定和性质;正确作出辅助线是解答本题的关键.

练习册系列答案
相关题目
17.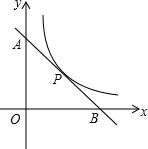 如图,一次函数y=-2x+4的图象与坐标轴分别交于A、B两点,点P在直线AB上运动(点P不与A,B两点重合),反比例函数y=$\frac{k}{x}$过点P,求k的最大值( )
如图,一次函数y=-2x+4的图象与坐标轴分别交于A、B两点,点P在直线AB上运动(点P不与A,B两点重合),反比例函数y=$\frac{k}{x}$过点P,求k的最大值( )
 如图,一次函数y=-2x+4的图象与坐标轴分别交于A、B两点,点P在直线AB上运动(点P不与A,B两点重合),反比例函数y=$\frac{k}{x}$过点P,求k的最大值( )
如图,一次函数y=-2x+4的图象与坐标轴分别交于A、B两点,点P在直线AB上运动(点P不与A,B两点重合),反比例函数y=$\frac{k}{x}$过点P,求k的最大值( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
4.将1:10000的某幅地图,表示范围不变,图幅放大为原来的4倍,新地图的比例尺为( )
| A. | 五千分之一 | B. | 图上一厘米代表实地距离5000米 | ||
| C. | 1:1000 | D. | $\frac{1}{20000}$ |
 如图,在△ABC中,BC=3cm,∠BAC=60°,那么△ABC外接圆的半径为$\sqrt{3}$cm.
如图,在△ABC中,BC=3cm,∠BAC=60°,那么△ABC外接圆的半径为$\sqrt{3}$cm.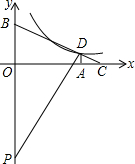 如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=$\frac{1}{2}$.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,PD与x轴交于点E,OA=8,OB=6.
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=$\frac{1}{2}$.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,PD与x轴交于点E,OA=8,OB=6.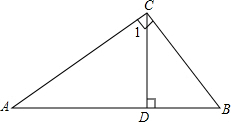 如图所示,在△ACB中,∠ACB=90°,∠1=∠B.
如图所示,在△ACB中,∠ACB=90°,∠1=∠B.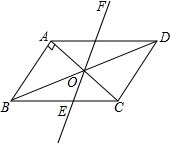 如图,?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
如图,?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.