题目内容
20.(1)计算:($\frac{1}{2}$)-1-4sin60°+$\sqrt{27}$+(3-π)0;(2)化简:($\frac{{a}^{2}-{b}^{2}}{{a}^{2}-2ab+{b}^{2}}$+$\frac{a}{b-a}$)÷$\frac{{b}^{2}}{{a}^{2}-ab}$.
分析 (1)根据负指数幂,特殊角的三角函数值,算术平方根以及零指数幂进行计算即可;
(2)先算括号里面的,再进行分式的约分即可.
解答 解:(1)原式=2-4×$\frac{\sqrt{3}}{2}$+3$\sqrt{3}$+1
=3+$\sqrt{3}$;
(2)原式=[$\frac{(a+b)(a-b)}{(a-b)^{2}}$-$\frac{a}{a-b}$]×$\frac{a(a-b)}{{b}^{2}}$
=($\frac{a+b}{a-b}$-$\frac{a}{a-b}$)×$\frac{a(a-b)}{{b}^{2}}$
=$\frac{a+b}{a-b}$×$\frac{a(a-b)}{{b}^{2}}$
=$\frac{ab}{{b}^{2}}$
=$\frac{a}{b}$.
点评 本题考查了分式的混合运算,掌握分式的通分、约分,负指数幂,特殊角的三角函数值,算术平方根以及零指数幂是解题的关键.

练习册系列答案
相关题目
15.函数y=-x+1、y=$\frac{3}{x}$、y=x2+x-2,y随x的增大而减小的有( )个.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.已知x=3是关于x的方程:4x-a=3+ax的解,那么a的值是( )
| A. | 2 | B. | $\frac{9}{4}$ | C. | 3 | D. | $\frac{9}{2}$ |
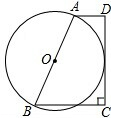 如图,在梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O,求证:CD是⊙O的切线.
如图,在梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O,求证:CD是⊙O的切线.