题目内容
10.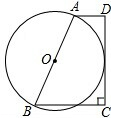 如图,在梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O,求证:CD是⊙O的切线.
如图,在梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O,求证:CD是⊙O的切线.
分析 首先过点O作OE⊥CD于点E,易证得OE是梯形ABCD的中位线,可得OE=$\frac{1}{2}$(AD+BC),又由AD+BC=AB,以AB为直径作⊙O.可得OE等于⊙O的半径.
解答 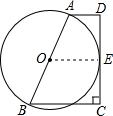 证明:过点O作OE⊥CD于点E,
证明:过点O作OE⊥CD于点E,
∵在梯形ABCD中,AD∥BC,∠C=90°,
∴AD⊥CD,BC⊥CD,
∴AD∥OE∥BC,
∵OA=OB,
∴OE是梯形ABCD的中位线,
∴OE=$\frac{1}{2}$(AD+BC),
∵AD+BC=AB,
∴OE=$\frac{1}{2}$AB,
∵以AB为直径作⊙O.
∴直线CD是⊙O的切线.
点评 此题考查了切线的判定以及梯形的中位线的性质.此题难度适中,注意辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
18.已知△ABC中,∠A=40°,∠B=50°,那么△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
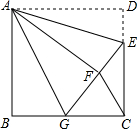 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,FC,下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,FC,下列结论: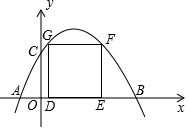 如图,抛物线l与坐标轴的交点为A(-1,0),B(4,0),C(0,2),四边形DEFG是正方形,且点D,E在x轴上,点F,G在抛物线上,则正方形DEFG的面积为57±8$\sqrt{41}$.
如图,抛物线l与坐标轴的交点为A(-1,0),B(4,0),C(0,2),四边形DEFG是正方形,且点D,E在x轴上,点F,G在抛物线上,则正方形DEFG的面积为57±8$\sqrt{41}$.