题目内容
16. 如图,平面直角坐标系中,把点A(-3,-1)向右平移5个单位得到B点,再把B点向上平移6个单位得到C点.
如图,平面直角坐标系中,把点A(-3,-1)向右平移5个单位得到B点,再把B点向上平移6个单位得到C点.(1)点O为坐标系原点.连接OA、OC、AC,求三角形AOC的面积S;
(2)设直线AC与y轴交于点M,现有一动点P从原点O出发,沿y轴的正方向向上运动,速度为每秒0.2个单位长度,运动时间为t秒,求点P在线段OM上和在线段OM外运动时,t的取值范围.
分析 (1)根据平移的性质得到C(2,5),由待定系数法确定直线AC的解析式为y=$\frac{6}{5}$x+$\frac{13}{5}$,得到M(0,$\frac{13}{5}$),于是得到结论;
(2)由OM=$\frac{13}{5}$,点P速度为每秒0.2个单位长度,即可得到结论.
解答 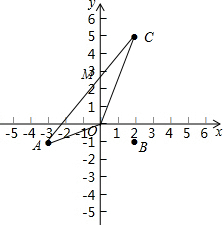 解:(1)∵点A(-3,-1)向右平移5个单位得到B点,再把B点向上平移6个单位得到C点,
解:(1)∵点A(-3,-1)向右平移5个单位得到B点,再把B点向上平移6个单位得到C点,
∴C(2,5),
设直线AC的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-1=-3k+b}\\{5=2k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{6}{5}}\\{b=\frac{13}{5}}\end{array}\right.$,
∴直线AC的解析式为y=$\frac{6}{5}$x+$\frac{13}{5}$,
∴M(0,$\frac{13}{5}$),
∴S△AOC=$\frac{1}{2}$×3×$\frac{13}{5}$+$\frac{1}{2}$×2×$\frac{13}{5}$=$\frac{13}{2}$;
(2)∵OM=$\frac{13}{5}$,点P速度为每秒0.2个单位长度,
∴①点P在线段OM上时,0≤t≤$\frac{13}{2}$,
②点P在线段OM外运动时,t>$\frac{13}{2}$.
点评 本题考查了坐标与图形变换-平移,坐标与图形的性质,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
1.三角形的三边长分别是3,1+2a,8,则数a的取值范围是( )
| A. | -2<a<4 | B. | 1<a<3.5 | C. | 2<a<5 | D. | 4<a<5 |
5.计算(-3)m+2×(-3)m-1,得( )
| A. | 3m-1 | B. | (-3)m-1 | C. | -(-3)m-1 | D. | (-3)m |
6.下列各式正确的是( )
| A. | ($\frac{1}{4}$)2=$\frac{1}{2}$ | B. | $\sqrt{2\frac{1}{4}}$=1$\frac{1}{2}$ | C. | $\sqrt{4+\frac{9}{16}}$=2+$\frac{3}{4}$=2$\frac{3}{4}$ | D. | $\sqrt{1{3}^{2}-{7}^{2}}$=13-7=6 |
 如图,已知A($2\sqrt{3}$,2)、B($2\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2$\sqrt{2}$,2$\sqrt{2}$)的位置,则图中阴影部分的面积为$\frac{7}{8}π$.
如图,已知A($2\sqrt{3}$,2)、B($2\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2$\sqrt{2}$,2$\sqrt{2}$)的位置,则图中阴影部分的面积为$\frac{7}{8}π$.
 如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为8.
如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为8. 在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF,并写出点E,F的坐标.
在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF,并写出点E,F的坐标.


