题目内容
15. 如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1≥y2的x的取值范围为( )
如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1≥y2的x的取值范围为( )| A. | x≥1 | B. | x≥2 | C. | x≤1 | D. | x≤2 |
分析 在图中找到两函数图象的交点,根据一次函数图象的交点坐标与不等式组解集的关系即可作出判断.
解答 解:∵直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),
∴当x=1时,y1=y2=2;
∴当y1≥y2时,x≥1.
故选A.
点评 此题考查了直线交点坐标与一次函数组成的不等式组的解的关系,利用图象即可直接解答,体现了数形结合思想在解题中的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.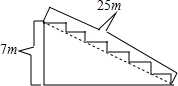 如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.
如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.
 如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.
如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.| A. | 21 | B. | 75 | C. | 93 | D. | 96 |
7.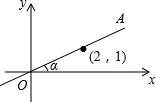 如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
 如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
4.已知a<b,下列不等式中,变形正确的是( )
| A. | a-3>b-3 | B. | $\frac{a}{3}>\frac{b}{3}$ | C. | -3a>-3b | D. | 3a-1>3b-1 |
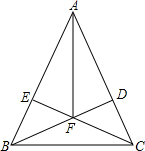 如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.试说明AF平分∠BAC的理由.
如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.试说明AF平分∠BAC的理由.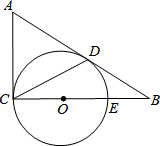 如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3.
如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3. 如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.