Question

6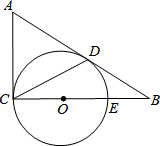．如图，在△ABC中，∠ACB=90°，以CE为直径作⊙O，AB与⊙O相切于点D，连接CD，若BE=OE=3．
（1）求证：∠A=2∠DCB；
（2）求线段AD的长度．

Answer 1

分析 （1）连接OD，求出∠ODB=90°，求出∠B=30°，∠DOB=60°，求出∠DCB度数，关键三角形内角和定理求出∠A，即可得出答案；
（2）根据勾股定理求出BD，设AD为x，利用勾股定理列出方程解答即可．

解答 （1）证明：连接OD，

则∠ODB=90°，
∴∠BOD+∠B=90°，
∵∠A+∠B=90°，
∴∠A=∠BOD，
∵OC=OD，
∴∠BOD=2∠DCB，
∴∠A=2∠DCB；
（2）解：如图，连接AO，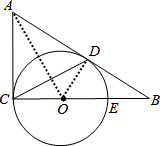

则△ACO≌△ADO，
∴AD=AC，
在△OBD中，BD=$\sqrt{O{B^2}-O{D^2}}$=$3\sqrt{3}$，
设AD=x，则AB=$3\sqrt{3}$+x，AC=x，BC=9，
${（3\sqrt{3}+x）^2}={x^2}+{9^2}$，
∴$x=3\sqrt{3}$，即AD=$3\sqrt{3}$．

点评 本题考查了含30度角的直角三角形性质，勾股定理，扇形的面积，勾股定理，切线的性质等知识点的应用，主要考查学生综合性运用性质进行推理和计算的能力．