题目内容
7.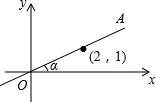 如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 设(2,1)点是B,作BC⊥x轴于点C,根据三角函数的定义即可求解.
解答  解:设(2,1)点是B,作BC⊥x轴于点C.
解:设(2,1)点是B,作BC⊥x轴于点C.
则OC=2,BC=1,
则tanα=$\frac{BC}{OC}$=$\frac{1}{2}$.
故选C.
点评 本题考查了三角函数的定义,理解正切函数的定义是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1≥y2的x的取值范围为( )
如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1≥y2的x的取值范围为( )
 如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1≥y2的x的取值范围为( )
如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1≥y2的x的取值范围为( )| A. | x≥1 | B. | x≥2 | C. | x≤1 | D. | x≤2 |
19.已知(a+3)2+$\sqrt{2b-1}$=0,则一次函数y=ax+b的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
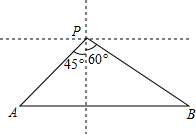 如图,一海伦位于灯塔P的西南方向,距离灯塔40$\sqrt{2}$海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).
如图,一海伦位于灯塔P的西南方向,距离灯塔40$\sqrt{2}$海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).