题目内容
10．
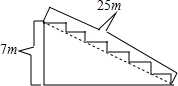如图，某公司举行周年庆典，准备在门口长25米，高7米的台阶上铺设红地毯，已知台阶的宽为3米，则共需购买（ ）m2的红地毯．| A． | 21 | B． | 75 | C． | 93 | D． | 96 |
分析 首先可利用勾股定理解图中直角三角形得台阶的地面长度为24米，则通过观察梯子可知需买红地毯的总长度为24+7=31米．
解答 解：依题意图中直角三角形一直角边为7米，斜边为25米，
根据勾股定理另一直角边长：$\sqrt{2{5}^{2}-{7}^{2}}$=24（米），
则需购买红地毯的长为24+7=31（米），
红地毯的宽则是台阶的宽3米，所以面积是：31×3=93（平方米）．
故选：C．
点评 本题考查了勾股定理的应用，善于观察题目的信息求出地毯的长度是解题关键．
练习册系列答案
相关题目
如图，△ABC中，AB=AC，且AC上的中线BD把这个三角形的周长分成了12cm和6cm的两部分，求这个三角形的腰长和底边的长．
15．
如图，直线y1=k1x+a与y2=k2x+b的交点坐标为（1，2），则使y1≥y2的x的取值范围为（ ）
如图，直线y1=k1x+a与y2=k2x+b的交点坐标为（1，2），则使y1≥y2的x的取值范围为（ ）| A． | x≥1 | B． | x≥2 | C． | x≤1 | D． | x≤2 |
19．已知（a+3）2+$\sqrt{2b-1}$=0，则一次函数y=ax+b的图象不经过的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |