题目内容
11.解方程组(1)$\left\{\begin{array}{l}{3x-13y=-16}\\{x+3y=2}\end{array}\right.$(用代入法)
(2)$\left\{\begin{array}{l}{x+3y=-1}\\{3x-2y=8}\end{array}\right.$(用加减法)
分析 (1)把②变形为x=2-3y代入①可得出y的值;再把y的值代入②可得出x的值;
(2)先用加减消元法求出y的值,进而可得出x的值.
解答 解:(1)$\left\{\begin{array}{l}{3x-13y=-16①}\\{x+3y=2②}\end{array}\right.$,②可化为x=2-3y,代入①得,3(2-3y)-13y=-16,解得y=1,
把y=1代入②得,x+3=2,解得x=-1,
故方程组的解为:$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+3y=-1①}\\{3x-2y=8②}\end{array}\right.$,①×3-②得,11y=-11,解得y=-1;①×2+2×3得,11x=22,解得x=2,
故方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.

练习册系列答案
相关题目
2.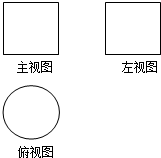 如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
 如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | π | D. | $\frac{3π}{2}$ |
19.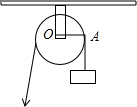 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )| A. | 5πcm | B. | 3πcm | C. | 2πcm | D. | πcm |
16.下列说法错误的是( )
| A. | 斜边及一锐角分别相等的两个直角三角形全等 | |
| B. | 两条直角边分别相等的两个直角三角形全等 | |
| C. | 两个锐角分别相等的两个直角三角形全等 | |
| D. | 一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等 |
20.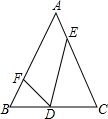 如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
 如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )| A. | 5.5 | B. | 4 | C. | 4.5 | D. | 3.5 |
1.在Rt△ABC中,∠C=90°,当∠A的度数不断增大时,cosA的值的变化情况是( )
| A. | 不断变大 | B. | 不断减小 | C. | 不变 | D. | 不能确定 |
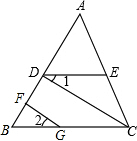 已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.
已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.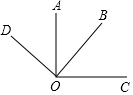 如图所示,∠AOB=42°,OA⊥OC,OB⊥OD,则∠COD=138°.
如图所示,∠AOB=42°,OA⊥OC,OB⊥OD,则∠COD=138°.