题目内容
20.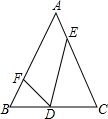 如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )| A. | 5.5 | B. | 4 | C. | 4.5 | D. | 3.5 |
分析 注意到△BDF与△CED相似,利用相似比求出BF,然后得出AF的长度.
解答 解:∵AB=AC,
∴∠B=∠C,
∵∠FDE=∠B,
∴∠BDF+∠BFD=∠BDF+∠EDC,
∴∠BFD=∠CDE,
∴△BDF∽△CED,
∴$\frac{BF}{CD}=\frac{BD}{CE}$,
∴$\frac{BF}{3}=\frac{2}{4}$,
∴BF=1.5,
∴AF=AB-BF=AC-BF=AE+CE-BF=4.
故选B.
点评 本题主要考查了相似三角形的判定与性质、等腰三角形的性质,属于基础题.识别出图形中的“一线三等角”模型从而得出三角形相似是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.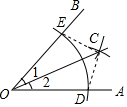 数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,两弧交于点C;(3)作射线OC并连接CD,CE,下列结论不正确的是( )
数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,两弧交于点C;(3)作射线OC并连接CD,CE,下列结论不正确的是( )
 数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,两弧交于点C;(3)作射线OC并连接CD,CE,下列结论不正确的是( )
数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,两弧交于点C;(3)作射线OC并连接CD,CE,下列结论不正确的是( )| A. | ∠1=∠2 | B. | S△OCE=S△OCD | C. | OD=CD | D. | OC垂直平分DE |
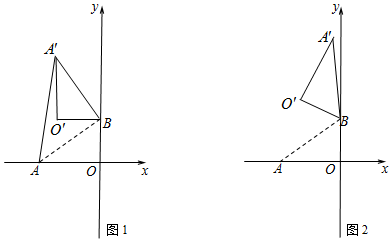
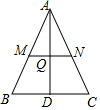 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AD=BC=1.点Q是AD上的一个动点,过点Q垂直于AD的直线分别交AB、AC于M、N两点,设AQ=x,△AMN的面积为y,则y关于x的函数图象大致形状是( )
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AD=BC=1.点Q是AD上的一个动点,过点Q垂直于AD的直线分别交AB、AC于M、N两点,设AQ=x,△AMN的面积为y,则y关于x的函数图象大致形状是( )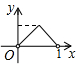
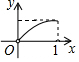
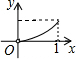
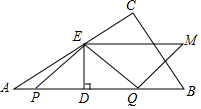 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=3cm,动点P、Q分别从点A、B同时出发,点P以1cm/s的速度沿A→B向终点B运动.点Q以2cm/s的速度沿B→向终点A运动.过QP的中点D作DE⊥AB交AC于点E.将△PQE绕着EQ的中点旋转180°得到△MEQP.设四边形QMEP的面积为S(cm2),点P运动的时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=3cm,动点P、Q分别从点A、B同时出发,点P以1cm/s的速度沿A→B向终点B运动.点Q以2cm/s的速度沿B→向终点A运动.过QP的中点D作DE⊥AB交AC于点E.将△PQE绕着EQ的中点旋转180°得到△MEQP.设四边形QMEP的面积为S(cm2),点P运动的时间为t(s).