题目内容
1. 已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.
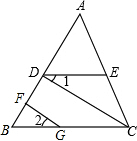
已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.求证:∠1=∠2.
证明:∵CD⊥AB,GF⊥AB.(已知)
∴∠BDC=∠BFG=90°.(垂直的定义)
∴CD∥GF.(同位角相等,两直线平行)
∴∠2=∠DCB.(两线平行,同位角相等)
∵∠B=∠ADE.(已知)
∴DE∥BC.(同位角相等,两直线平行)
∴∠1=(∠BCD)(两条直线平行,内错角相等)
∴∠1=∠2.(等量代换)
分析 由CD⊥AB,GF⊥AB,根据平行线的判定方法得CD∥GF,再根据平行线的性质得∠2=∠BCD;由∠B=∠ADE,根据同位角相等,两直线平行得DE∥BC,则利用平行线的性质得∠1=∠BCD,然后利用等量代换即可得到∠1=∠2.
解答 证明:∵CD⊥AB,GF⊥AB,(已知)
∴∠BDC=∠BFG(垂直的定义)
∴CD∥GF,(同位角相等,两直线平行)
∴∠2=∠BCD,(两线平行,同位角相等)
∵∠B=∠ADE,(已知)
∴DE∥BC,(同位角相等,两直线平行)
∴∠1=∠BCD,
∴∠1=∠2.(等量代换)
故答案为垂直的定义,同位角相等,两直线平行,两线平行,同位角相等;同位角相等,两直线平行;∠DCB;等量代换.
点评 本题考查了平行线的判定与性质:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
 将一块直角三角板与一两边平行的纸条按如图所示位置放置,若∠1=20°,则∠2=70°.
将一块直角三角板与一两边平行的纸条按如图所示位置放置,若∠1=20°,则∠2=70°.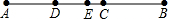 如图,点C为线段AB上一点,若线段AC=12cm,AC=$\frac{3}{2}$BC,D、E两点分别为AC、AB的中点,则DE的长为4cm.
如图,点C为线段AB上一点,若线段AC=12cm,AC=$\frac{3}{2}$BC,D、E两点分别为AC、AB的中点,则DE的长为4cm. 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为36cm2,则△BEF的面积=9cm2.
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为36cm2,则△BEF的面积=9cm2.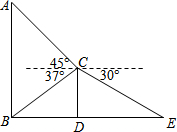 某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.