已知2+$\sqrt{1-y}$=0.则x+y=-1．题目和参考答案——青夏教育精英家教网—

题目内容

1．已知（x-y+3）²+$\sqrt{1-y}$=0，则x+y=-1．

分析直接利用偶次方的性质结合绝对值的性质得出x，y的值，即可得出答案．

解答解：∵（x-y+3）²+$\sqrt{1-y}$=0，
∴$\left\{\begin{array}{l}{x-y+3=0}\\{1-y=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$，
则x+y=-1．
故答案为：-1．

点评此题主要考查了偶次方的性质以及绝对值的性质，得出x，y的等式是解题关键．

练习册系列答案

12．在△ABC中，若|sinB-$\frac{\sqrt{2}}{2}$|+$\sqrt{1-tanA}$=0，则△ABC是（　　）

9．下列运算不正确的有（　　）
①x⁴•x³=x¹²
②（x³）⁴=x⁸¹
③x⁴÷x³=x（x≠0）
④x⁴+x³=x⁷．

16．已知m²+6mn+9n²+|n-3|=0，则m=-9，n=3．

6．解关于x的一元二次方程
（1）2x²-ax=15a²
（2）4（x-2）²-25（x+2）²=0．

13．

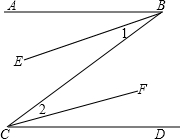在下面的括号内，填上推理的根据：如图，已知AB∥CD，BE平分∠ABC，CF平分∠BCD，求证：BE∥CF．
证明：∵AB∥CD，（已知）
∴∠ABC=∠BCD．（两直线平行，内错角相等）
∵BE平分∠ABC，CF平分∠BCD，（已知）
∴∠1=$\frac{1}{2}$∠ABC，∠2=$\frac{1}{2}$∠DCB（角平分线定义）
∴∠1=∠2．
∴BE∥CF．（内错角相等，两直线平行）

10．若（x-3）²+（3y+1）²=0，则x²⁰¹⁶•y²⁰¹⁷=-$\frac{1}{3}$．

11．计算：
（1）$\frac{1}{{\sqrt{3}+1}}-\frac{{\sqrt{3}}}{2}+\sqrt{32}×\sqrt{\frac{1}{8}}$
（2）$（\sqrt{3}+3\sqrt{2}-\sqrt{6}）（\sqrt{3}-\sqrt{6}-3\sqrt{2}）$．

试题分类