题目内容
13.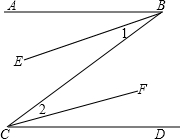 在下面的括号内,填上推理的根据:如图,已知AB∥CD,BE平分∠ABC,CF平分∠BCD,求证:BE∥CF.
在下面的括号内,填上推理的根据:如图,已知AB∥CD,BE平分∠ABC,CF平分∠BCD,求证:BE∥CF.证明:∵AB∥CD,(已知)
∴∠ABC=∠BCD.(两直线平行,内错角相等)
∵BE平分∠ABC,CF平分∠BCD,(已知)
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠DCB(角平分线定义)
∴∠1=∠2.
∴BE∥CF.(内错角相等,两直线平行)
分析 根据平行线的性质得出∠ABC=∠BCD,求出∠1=∠2,根据平行线的判定得出即可.
解答 证明:∵AB∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等),
∵BE平分∠ABC,CF平分∠BCD(已知),
∴∠1=$\frac{1}{2}$∠∠ABC,∠2=$\frac{1}{2}$∠DCB(角平分线定义)
∴∠1=∠2.
∴BE∥CF(内错角相等,两直线平行),
故答案为:两直线平行,内错角相等,ABC,DCB,角平分线定义,内错角相等,两直线平行.
点评 本题考查了平行线的性质和判定的应用,能求出∠1=∠2是解此题的关键,注意:两直线平行,内错角相等,反之亦然.

练习册系列答案
相关题目
4.若直线y1=m2x+a与直线y2=-2x+b的交点坐标为(1,2),则使y1<y2成立的x的取值范围为( )
| A. | x>1 | B. | x>2 | C. | x<1 | D. | x<2 |
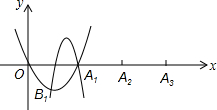 如图,已知在平面直角坐标系中,x轴上依次有点A1(2,0),A2(4,0),A3(6,0),…,抛物线l1:y=x2+bx+c经过原点及A1,顶点为B1;抛物线l2经过B1和A1,且形状与抛物线l1的形状相同,开口方向相反;抛物线l3经过A1和A2,且形状与抛物线l2的形状相同,开口方向相反,顶点为B2:抛物线l4经过B2和A2,且形状与抛物线l3的形状相同,开口方向相反:抛物线l5经过A2和A3,且形状与抛物线l4的形状相同,开口方向相反,顶点为B3:依此类推…
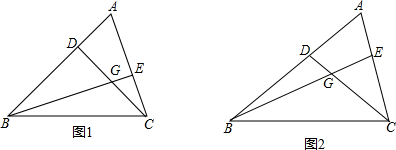
如图,已知在平面直角坐标系中,x轴上依次有点A1(2,0),A2(4,0),A3(6,0),…,抛物线l1:y=x2+bx+c经过原点及A1,顶点为B1;抛物线l2经过B1和A1,且形状与抛物线l1的形状相同,开口方向相反;抛物线l3经过A1和A2,且形状与抛物线l2的形状相同,开口方向相反,顶点为B2:抛物线l4经过B2和A2,且形状与抛物线l3的形状相同,开口方向相反:抛物线l5经过A2和A3,且形状与抛物线l4的形状相同,开口方向相反,顶点为B3:依此类推… 设△ABC是锐角三角形,∠A,∠B所对的边长分别为a、b,其边上的高分别为m,n,∠ACB=θ.
设△ABC是锐角三角形,∠A,∠B所对的边长分别为a、b,其边上的高分别为m,n,∠ACB=θ. 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2的坐标是(2$\sqrt{3}$,4).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2的坐标是(2$\sqrt{3}$,4).