题目内容
11.计算:(1)$\frac{1}{{\sqrt{3}+1}}-\frac{{\sqrt{3}}}{2}+\sqrt{32}×\sqrt{\frac{1}{8}}$
(2)$(\sqrt{3}+3\sqrt{2}-\sqrt{6})(\sqrt{3}-\sqrt{6}-3\sqrt{2})$.
分析 (1)首先化简二次根式进而合并同类二次根式得出答案即可;
(2)直接利用平方差公式计算得出答案.
解答 解:(1)原式=$\frac{{\sqrt{3}-1}}{3-1}-\frac{{\sqrt{3}}}{2}+\sqrt{32×\frac{1}{8}}$
=$\frac{{\sqrt{3}-1}}{2}-\frac{{\sqrt{3}}}{2}+2$
=$\frac{{\sqrt{3}}}{2}-\frac{1}{2}-\frac{{\sqrt{3}}}{2}+2$
=$\frac{3}{2}$;
(2)原式=$(\sqrt{3}-\sqrt{6}+3\sqrt{2})(\sqrt{3}-\sqrt{6}-3\sqrt{2})$
=$(\sqrt{3}-\sqrt{6}{)^2}-(3\sqrt{2}{)^2}$
=$3-6\sqrt{2}+6-18$
=$-9-6\sqrt{2}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
16.-2,0,0.5,-$\sqrt{2}$这四个数中,属于无理数的是( )
| A. | -2 | B. | 0 | C. | 0.5 | D. | -$\sqrt{2}$ |
1.观察下列各数:1,1,$\frac{5}{7}$,$\frac{7}{15}$,$\frac{9}{31}$,…按你发现的规律计算这列数的第7个数为( )
| A. | $\frac{15}{255}$ | B. | $\frac{13}{127}$ | C. | $\frac{11}{127}$ | D. | $\frac{11}{63}$ |
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2的坐标是(2$\sqrt{3}$,4).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2的坐标是(2$\sqrt{3}$,4).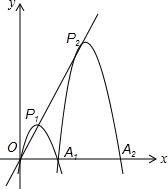 已知在平面直角坐标系xOy中,抛物线y1=ax2+bx(a≠0),与x轴正半轴交于点A1(2,0),顶点为P1,△OP1A1为正三角形,现将抛物线y1=ax2+bx(a≠0)沿射线OP1平移,把过点A1时的抛物线记为抛物线y2,记抛物线y2与x轴的另一交点为A2;把抛物线y2继续沿射线OP1平移,把过点A2时的抛物线记为抛物线y3,记抛物线y3与x轴的另一交点为A3;….;把抛物线y2015继续沿射线OP1平移,把过点A2015时的抛物线记为抛物线y2016,记抛物线y2016与x轴的另一交点为A2016,顶点为P2016.若这2016条抛物线的顶点都在射线OP1上.
已知在平面直角坐标系xOy中,抛物线y1=ax2+bx(a≠0),与x轴正半轴交于点A1(2,0),顶点为P1,△OP1A1为正三角形,现将抛物线y1=ax2+bx(a≠0)沿射线OP1平移,把过点A1时的抛物线记为抛物线y2,记抛物线y2与x轴的另一交点为A2;把抛物线y2继续沿射线OP1平移,把过点A2时的抛物线记为抛物线y3,记抛物线y3与x轴的另一交点为A3;….;把抛物线y2015继续沿射线OP1平移,把过点A2015时的抛物线记为抛物线y2016,记抛物线y2016与x轴的另一交点为A2016,顶点为P2016.若这2016条抛物线的顶点都在射线OP1上.