题目内容
18.已知关于x的方程(a+1)x=2ax-a2的解是负数,那么a的取值范围是a<1.分析 首先解关于x的方程,利用a表示出x的值,然后利用方程的解是负数列不等式求得a的范围.
解答 解:移项,得(a+1)x-2ax=-a2,
合并同类项,得(1-a)x=-a2,
系数化成1得x=$\frac{{a}^{2}}{a-1}$,
∵方程的解是负数,
∴a-1<0,
解得a<1.
故答案是:a<1.
点评 本题考查了方程的解与不等式,正确解关于x的方程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.要使式子$\sqrt{x-1}$在实数范围内有意义,字母x必须满足的条件是( )
| A. | x≥1 | B. | x≤1 | C. | x>1 | D. | x<1 |
3.在直线AB上取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数( )
| A. | 60° | B. | 90° | C. | 120° | D. | 60°或120° |
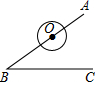 如图,∠ABC=60°,O为BA上一个动点,若⊙O的半径为6,则当OB=4$\sqrt{3}$时⊙O与BC相切.
如图,∠ABC=60°,O为BA上一个动点,若⊙O的半径为6,则当OB=4$\sqrt{3}$时⊙O与BC相切. 一只小狗在如图所示的方砖上走动,每块方砖的面积相等,则小狗最终停在阴影方砖上的概率是$\frac{1}{3}$.
一只小狗在如图所示的方砖上走动,每块方砖的面积相等,则小狗最终停在阴影方砖上的概率是$\frac{1}{3}$.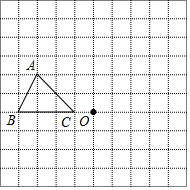 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).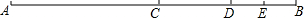 如图所示,已知AB=40,点C是线段AB的中点,点D是线段CB上的一点,点E为线段DB的中点,EB=6,求线段CD的长.
如图所示,已知AB=40,点C是线段AB的中点,点D是线段CB上的一点,点E为线段DB的中点,EB=6,求线段CD的长.