题目内容
8.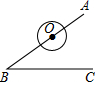 如图,∠ABC=60°,O为BA上一个动点,若⊙O的半径为6,则当OB=4$\sqrt{3}$时⊙O与BC相切.
如图,∠ABC=60°,O为BA上一个动点,若⊙O的半径为6,则当OB=4$\sqrt{3}$时⊙O与BC相切.
分析 设⊙O与BC相切于点D,连接OD,在Rt△OBD中可求得OB的长.
解答  解:
解:
设⊙O与BC相切于点D,连接OD,
则可知OD⊥BC,
∵∠ABC=60°,
∴$\frac{OD}{OB}$=sin60°,
∴OB=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题主要考查直线和圆的位置关系,掌握过切点的半径与切线垂直是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
3.比2的相反数小的是( )
| A. | 5 | B. | -3 | C. | 0 | D. | -1 |
19.下列计算正确的是( )
| A. | a4b-6a3b+9a2b=a2b(a2-6a+9) | B. | x2-2x+1=(x-1)2 | ||
| C. | x2-2x+4=(x-2)2 | D. | 4x2-y2=(4x+y)(4x-y) |
13.下列叙述正确的是( )
| A. | 平分弦的直径垂直于弦 | B. | 三角形的外心到三边的距离相等 | ||
| C. | 三角形的内心到三边的距离相等 | D. | 相等的圆周角所对的弧相等 |
17.下列各组数中,是勾股数的( )
| A. | 12,15,18 | B. | 11,60,61 | C. | 15,16,17 | D. | 12,35,36 |