题目内容
8.在矩形ABCD中,AB=3,BC=4,BD的垂直平分线交AD于E,则AE的长为$\frac{7}{8}$.分析 如图,连接BE.设AE=x,则DE=4-x.因为BD的垂直平分线交AD于E,所以EB=ED=4-x,在Rt△ABE中,根据AB2+AE2=BE2,列出方程即可解决问题.
解答 解:如图,连接BE.设AE=x,则DE=4-x.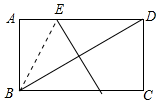
∵四边形ABCD是矩形,
∴AD=CB=4,∠A=90°,
∵BD的垂直平分线交AD于E,
∴EB=ED=4-x,
在Rt△ABE中,∵AB2+AE2=BE2,
∴32+x2=(4-x)2,
∴x=$\frac{7}{8}$,
∴AE=$\frac{7}{8}$.
故答案为$\frac{7}{8}$.
点评 本题考查矩形的性质、线段的垂直平分线的性质、勾股定理等知识,解题的关键是学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
19.两个正数与一个负数相加,和为( )
| A. | 正数 | B. | 负数 | C. | 零 | D. | 以上都有可能 |

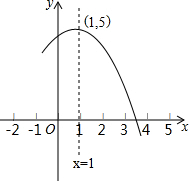 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,5)且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,5)且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论: