题目内容
7.在平面直角坐标系xOy中,已知点P在第二象限,且其坐标为(a,$\sqrt{5}$),若PO=2$\sqrt{3}$,则a=-$\sqrt{7}$.分析 利用勾股定理列出方程并根据第二象限点的横坐标是负数求解即可.
解答 解:根据勾股定理得,PO=$\sqrt{{a}^{2}+(\sqrt{5})^{2}}$=2$\sqrt{3}$,
所以a2=7,
∵点P在第二象限,
∴a<0,
∴a=-$\sqrt{7}$.
故答案为:-$\sqrt{7}$.
点评 本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
相关题目
17.下列各组数中,是勾股数的( )
| A. | 12,15,18 | B. | 11,60,61 | C. | 15,16,17 | D. | 12,35,36 |
15.下列运算中正确的是( )
| A. | 2a+3a2=5a3 | B. | (-2a2)3=-8a6 | C. | a2•a3=a6 | D. | a8÷a2=a4 |
2.下列四个实数中,是无理数的为( )
| A. | 0 | B. | $\sqrt{2}$ | C. | -5 | D. | $\frac{3}{7}$ |
19.两个正数与一个负数相加,和为( )
| A. | 正数 | B. | 负数 | C. | 零 | D. | 以上都有可能 |
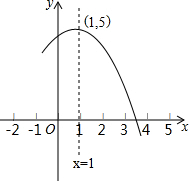 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,5)且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,5)且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论: