题目内容
3.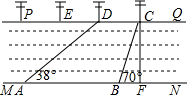 如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).
如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).
分析 过点C作CG∥DA交AB于点F,易证四边形AGCD是平行四边形.再在直角△CBF中,利用三角函数求解.
解答 解:过点C作CG∥DA交AB于点G.
如图,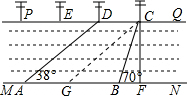
∵MN∥PQ,CG∥DA,
∴四边形AGCD是平行四边形.
∴AG=CD=50m,∠CGB=38°.
∴GB=AB-AG=120-50=70(m).
∴tan38°=$\frac{CF}{70+BF}$=0.78,
在Rt△BFC中,
tan70°=$\frac{CF}{BF}$=2.75,
∴BF=$\frac{CF}{2.75}$,
∴$\frac{CF}{70+BF}=\frac{CF}{70+\frac{CF}{2.75}}$=0.78,
解得:CF≈76.2(m).
答:河流的宽是76.2米.
点评 此题主要考查了解直角三角形的应用,不规则图形可以通过作平行线转化为平行四边形与直角三角形的问题进行解决.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
15.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x的值为( )
| A. | 0 | B. | ±1 | C. | 1 | D. | -1 |
 一个三角形各顶点的坐标如图所示,把此三角形先向左平移3个单位长度,再向上平移2个单位长度得到三角形A′B′C′,
一个三角形各顶点的坐标如图所示,把此三角形先向左平移3个单位长度,再向上平移2个单位长度得到三角形A′B′C′,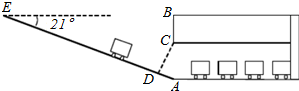 某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).(参考数据:sin21°≈0.28,cos21°≈0.91,tan21°≈0.43)
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).(参考数据:sin21°≈0.28,cos21°≈0.91,tan21°≈0.43)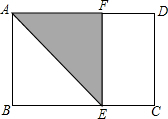 将长为1,宽为a的矩形纸片ABCD($\frac{1}{2}$<a<1)按如图方式折叠,剪下一个边长等于矩形宽度的正方形ABEF.若剩下的矩形EFDC与矩形ABCD相似,则a=$\frac{1+\sqrt{5}}{2}$.
将长为1,宽为a的矩形纸片ABCD($\frac{1}{2}$<a<1)按如图方式折叠,剪下一个边长等于矩形宽度的正方形ABEF.若剩下的矩形EFDC与矩形ABCD相似,则a=$\frac{1+\sqrt{5}}{2}$. 如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.