题目内容
13.在△ABC中,∠C=90°,点D、E分别是边A以、BC上的点,点P是一动点,连接PD、PE,∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)如图1所示,若点P在线段AB上,且∠α=40°,则∠1+∠2=130°;
(2)如图2所示,若点P在边AB上运动,则∠α、∠1、∠2之间的关系为有何数量关系;猜想结论并说明理由;
(3)如图3所示,若点P运动到边AB的延长线上,则∠α、∠1、∠2之间有何数量关系?猜想结论并说明理由.
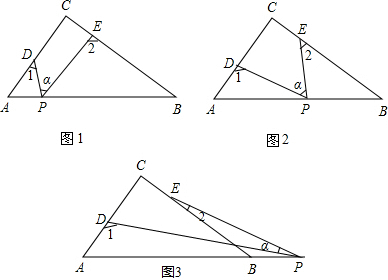
分析 (1)根据四边形内角和定理以及邻补角的定义得出∠1+∠2=∠C+∠α,进而得出即可;
(2)利用(1)中所求得出答案即可;
(3)利用三角外角的性质得出∠1=∠C+∠2+α=90°+∠2+α;
解答 解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=40°,
∴∠1+∠2=130°;
故答案为:130°;
(2)由(1)得出:
∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+α
故答案为:∠1+∠2=90°+α;
(3)∠1=90°+∠2+α,
理由:∵∠2+∠α=∠DME,∠DME+∠C=∠1,
∴∠1=∠C+∠2+α=90°+∠2+α.
点评 本题考查了三角形内角和定理和外角的性质、对顶角相等的性质,熟练利用三角形外角的性质是解题的关键.

练习册系列答案
相关题目
8. 将一副三角板(含30°、45°的直角三角形)摆放成如图所示的形状,图中∠1的度数是( )
将一副三角板(含30°、45°的直角三角形)摆放成如图所示的形状,图中∠1的度数是( )
 将一副三角板(含30°、45°的直角三角形)摆放成如图所示的形状,图中∠1的度数是( )
将一副三角板(含30°、45°的直角三角形)摆放成如图所示的形状,图中∠1的度数是( )| A. | 120° | B. | 130° | C. | 135° | D. | 150° |
18.以下说法正确的是( )
| A. | 在367人中至少有两个人的生日相同 | |
| B. | 一次摸奖活动的中奖率是1%,那么摸100次必然会中一次奖 | |
| C. | 一副扑克牌中,随意抽取一张是红桃K,这是必然事件 | |
| D. | 一个不透明的袋中装有3个红球,5个白球,搅匀后想中任意摸出一个球,摸到红球的可能性大于摸到白球的可能性 |
 如图,已知△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC相交于点F,如果AB=9,BD=3,那么CF的长度为2.
如图,已知△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC相交于点F,如果AB=9,BD=3,那么CF的长度为2.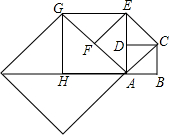 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为($\sqrt{2}$)n-1.
如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为($\sqrt{2}$)n-1.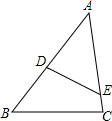 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,AB=3,△ADE的面积是4,则四边形BCED的面积是5.
如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,AB=3,△ADE的面积是4,则四边形BCED的面积是5.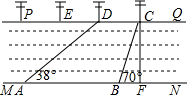 如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).
如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).