题目内容
8．若x1，x2是一元二次方程x2-2x-3=0的两个根，则x1x2的值是（ ）| A． | -2 | B． | -3 | C． | 2 | D． | 3 |
分析 由“x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$”可得x1x2=$\frac{c}{a}$，套入数据即可得出结论．
解答 解：∵x1，x2是一元二次方程x2-2x-3=0的两个根，
∴x1x2=$\frac{c}{a}$=$\frac{-3}{1}$=-3．
故选B．
点评 本题考查了根与系数的关系，解题的关键是能够熟练的使用根与系数的关系解决问题．本题属于基础题，难度不大，解决该题型题目时，由根与系数的关系得知x1x2=$\frac{c}{a}$，套入数据即可．
练习册系列答案
相关题目
18．
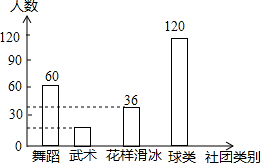某校开展社团活动，准备组件舞蹈、武术、球类（足球、篮球、乒乓球、羽毛球）．花样滑冰四类社团，为了解在校学生对这4个社团活动的喜爱情况，学校随机抽取部分学生进行了“你最喜爱的社团”调查，依据相关数据绘制以下的统计图表，请根据图表中的信息解答下列问题：
“你最喜爱的社团”调查统计图表
（1）被调查的学生总人数是240；m=24，n=15．
（2）被调查喜爱球类的学生中有12人最喜爱乒乓球，若该校有2600名学生，试估计全校最喜爱乒乓球的人数．
某校开展社团活动，准备组件舞蹈、武术、球类（足球、篮球、乒乓球、羽毛球）．花样滑冰四类社团，为了解在校学生对这4个社团活动的喜爱情况，学校随机抽取部分学生进行了“你最喜爱的社团”调查，依据相关数据绘制以下的统计图表，请根据图表中的信息解答下列问题：“你最喜爱的社团”调查统计图表
| 社团类别 | 人数 | 占总人数的比例 |
| 舞蹈 | 60 | 25% |
| 武术 | m | 10% |
| 花样滑冰 | 36 | n% |
| 球类 | 120 | 50% |
（2）被调查喜爱球类的学生中有12人最喜爱乒乓球，若该校有2600名学生，试估计全校最喜爱乒乓球的人数．
13．已知二次函数y=ax2-bx+$\frac{1}{2}$b-a与x轴交于A、B两点，则线段AB的最小值为（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | $\sqrt{3}$ | D． | 无法确定 |
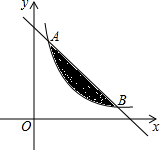平面直角坐标系中，我们把横坐标、纵坐标都是整数的点称为整点．如图，直线y=-x+7和反比例函数y=$\frac{6}{x}$（x＞0）的图象交于A，B两点，则落在图中阴影部分（不包含边界）内的整点个数有（ ）个．
17．射线AD、AE分别与⊙O相切于D、E两点，直线BC与⊙O相切于点F，分别交AD、AE于点B、C，若∠A=40°．则∠BOC等于（ ）
| A． | 70° | B． | 110° | C． | 70°或110° | D． | 40°或140° |
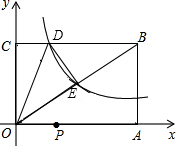如图，已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上，顶点B的坐标是（6，4），反比例函数y=$\frac{k}{x}$（x＞0）的图象经过矩形对角线的交点E，且与BC边交于点D．