题目内容
18.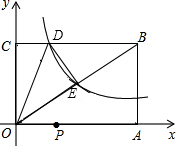 如图,已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,顶点B的坐标是(6,4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.
如图,已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,顶点B的坐标是(6,4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.(1)①求反比例函数的解析式与点D的坐标;
②直接写出△ODE的面积;
(2)若P是OA上的动点,求使得“PD+PE之和最小”时的直线PE的解析式.
分析 (1)①连接OE,则O、E、B三点共线,则E是OB的中点,即可求得E的坐标,利用待定系数法求得函数的解析式,进而求得D的坐标;
②根据S△ODE=S△OBC-S△OCD-S△BDE即可求解;
(2)作E关于OA轴的对称点E',则直线DE'就是所求的直线PE,利用待定系数法即可求解.
解答 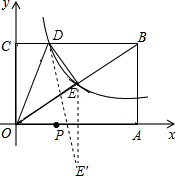 解:(1)①连接OB,则O、E、B三点共线.
解:(1)①连接OB,则O、E、B三点共线.
∵B的坐标是(6,4),E是矩形对角线的交点,
∴E的坐标是(3,2),
∴k=3×2=6,
则函数的解析式是y=$\frac{6}{x}$.
当y=4时,x=1.5,即D的坐标是(1.5,4);
②S△OBC=$\frac{1}{2}$BC•OC=$\frac{1}{2}$×6×4=12,
S△OCD=$\frac{1}{2}$OC•CD=$\frac{1}{2}$×4×1.5=3,
S△BDE=$\frac{1}{2}$×(6-1.5)×2=4.5,
则S△ODE=S△OBC-S△OCD-S△BDE=12-3-3-4.5=4.5;
(2)作E关于OA轴的对称点E',则E'的坐标是(3,-2).
连接E'D,与x轴交点是P,此时PO+PE最小.
设y=mx+n,把E'和D的坐标代入得:
$\left\{\begin{array}{l}{-2=3m+n}\\{4=1.5m+n}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-4}\\{n=10}\end{array}\right.$,
则直线DE'的解析式是y=-4x+10.
令y=0,则-4x+10=0,解得x=$\frac{5}{2}$,则P的坐标是($\frac{5}{2}$,0).
设PE的解析式是y=ax+b,
则$\left\{\begin{array}{l}{\frac{5}{2}a+b=0}\\{3a+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=4}\\{b=-10}\end{array}\right.$,
则直线PE的解析式是y=4x-10.
点评 本题考查了待定系数法求函数的解析式,以及图形的对称,求得函数的解析式是关键.

| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
| A. | -2 | B. | 2 | C. | 0 |
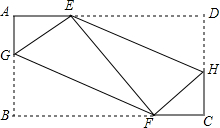 已知在矩形ABCD中,AB=4,AD=7,点G、F、H、E是分别边AB、BC、DC、AD上的点,分别沿HE,GF折叠矩形恰好使DE、BF都与EF重合,则AE=( )
已知在矩形ABCD中,AB=4,AD=7,点G、F、H、E是分别边AB、BC、DC、AD上的点,分别沿HE,GF折叠矩形恰好使DE、BF都与EF重合,则AE=( )| A. | 1或$\frac{8}{3}$ | B. | 2或$\frac{8}{3}$ | C. | $\frac{3}{2}$或$\frac{8}{3}$ | D. | $\frac{5}{2}$或$\frac{8}{3}$ |
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | -1+$\sqrt{2}$ | D. | 1-$\sqrt{2}$ |
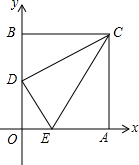 如图,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.
如图,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.