题目内容
13.已知二次函数y=ax2-bx+$\frac{1}{2}$b-a与x轴交于A、B两点,则线段AB的最小值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 无法确定 |
分析 设A(x1,0),B(x2,0).根据根与系数的关系和两点间的距离公式进行解答.
解答 解:设A(x1,0),B(x2,0).
依题意得 x1+x2=$\frac{b}{a}$,x1•x2=$\frac{1}{2}$$\frac{\frac{1}{2}(b-a)}{a}$=$\frac{b}{2a}$-1.
则AB=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(\frac{b}{a})^{2}-4(\frac{b}{2a}-1)^{\;}}$=$\sqrt{(\frac{b}{a}-1)^{2}+3}$≥$\sqrt{3}$.
故线段AB的最小值为$\sqrt{3}$,
故选C.
点评 本题考查了抛物线与x轴的交点.熟记完全平方公式和几个公式的变形是解题的关键.

练习册系列答案
相关题目
8.若x1,x2是一元二次方程x2-2x-3=0的两个根,则x1x2的值是( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
18.据国家统计局公告,2015年我国国内生产总值达到67.7亿元,将数67700000000000用科学记数法表示应为( )
| A. | 6.77×1012 | B. | 67.7×1012 | C. | 6.77×1013 | D. | 67.7×1013 |
5.北京新国际机场采用“海星”设计方案,航站楼主体与五座向外伸展的指廊总建筑面积为1 030 000平方米,将1030000用科学记数法表示应为( )
| A. | 103×104 | B. | 10.3×105 | C. | 1.03×105 | D. | 1.03×106 |
2.-2016的倒数的绝对值为( )
| A. | -2016 | B. | $-\frac{1}{2016}$ | C. | 2016 | D. | $\frac{1}{2016}$ |

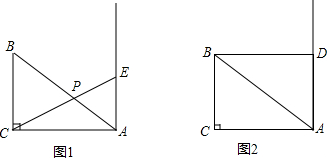 如图,△ABC中,∠ACB=90°,BC=6,AC=8.点E与点B在AC的同侧,且AE⊥AC.
如图,△ABC中,∠ACB=90°,BC=6,AC=8.点E与点B在AC的同侧,且AE⊥AC.