题目内容
17.射线AD、AE分别与⊙O相切于D、E两点,直线BC与⊙O相切于点F,分别交AD、AE于点B、C,若∠A=40°.则∠BOC等于( )| A. | 70° | B. | 110° | C. | 70°或110° | D. | 40°或140° |
分析 先画出符合的两个图形,根据切线的性质得出∠DBO=∠FBO,∠ECO=∠FCO,∠ODA=∠OEA=90°,∠OFB=∠OFC=90°,求出∠DOE的度数,即可求出答案.
解答 解:分为两种情况:第一种情况:如图1,连接OD、OF、OE, ∵射线AD、AE分别与⊙O相切于D、E两点,直线BC与⊙O相切于点F,
∵射线AD、AE分别与⊙O相切于D、E两点,直线BC与⊙O相切于点F,
∴∠DBO=∠FBO,∠ECO=∠FCO,∠ODA=∠OEA=90°,∠OFB=∠OFC=90°,
∵∠A=40°,
∴∠DOE=360°-90°-90°-40°=140°,
∵∠DBO=∠FBO,∠ECO=∠FCO,∠ODA=∠OEA=90°,∠OFB=∠OFC=90°,
∴根据三角形内角和定理得:∠DOB=∠FOB,∠EOC=∠FOC,
∴∠BOC=∠FOB+∠FOC
=$\frac{1}{2}$(∠DOF+∠EOF)
=$\frac{1}{2}$∠DOE
=$\frac{1}{2}×$140°
=70°;
第二种情况:如图2,
此时∠DOE=140°,
则∠BOC=$\frac{1}{2}$×(360°-140°)=110°;
故选C.
点评 本题考查了切线的性质,切线长定理的应用,能求出符合的两个情况是解此题的关键.

练习册系列答案
相关题目
8.若x1,x2是一元二次方程x2-2x-3=0的两个根,则x1x2的值是( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
5.北京新国际机场采用“海星”设计方案,航站楼主体与五座向外伸展的指廊总建筑面积为1 030 000平方米,将1030000用科学记数法表示应为( )
| A. | 103×104 | B. | 10.3×105 | C. | 1.03×105 | D. | 1.03×106 |
12. 在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.
在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.
(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
 在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.
在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
2.-2016的倒数的绝对值为( )
| A. | -2016 | B. | $-\frac{1}{2016}$ | C. | 2016 | D. | $\frac{1}{2016}$ |
9.-2的相反数是( )
| A. | -2 | B. | 2 | C. | 0 |
7.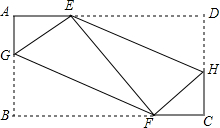 已知在矩形ABCD中,AB=4,AD=7,点G、F、H、E是分别边AB、BC、DC、AD上的点,分别沿HE,GF折叠矩形恰好使DE、BF都与EF重合,则AE=( )
已知在矩形ABCD中,AB=4,AD=7,点G、F、H、E是分别边AB、BC、DC、AD上的点,分别沿HE,GF折叠矩形恰好使DE、BF都与EF重合,则AE=( )
 已知在矩形ABCD中,AB=4,AD=7,点G、F、H、E是分别边AB、BC、DC、AD上的点,分别沿HE,GF折叠矩形恰好使DE、BF都与EF重合,则AE=( )
已知在矩形ABCD中,AB=4,AD=7,点G、F、H、E是分别边AB、BC、DC、AD上的点,分别沿HE,GF折叠矩形恰好使DE、BF都与EF重合,则AE=( )| A. | 1或$\frac{8}{3}$ | B. | 2或$\frac{8}{3}$ | C. | $\frac{3}{2}$或$\frac{8}{3}$ | D. | $\frac{5}{2}$或$\frac{8}{3}$ |
 如图,已知点A是一次函数y=x的图象与反比例函数y=$\frac{2}{x}$的图象在第一象限内的交点,点B在x轴的负半轴上且OA=OB.
如图,已知点A是一次函数y=x的图象与反比例函数y=$\frac{2}{x}$的图象在第一象限内的交点,点B在x轴的负半轴上且OA=OB.