题目内容
3.小明手中有长度分别为1cm,3cm,3cm,4cm和5cm的五根细木棒,现从中随机取出三根细木棒.(1)这三根细木棒能构成三角形的概率是$\frac{1}{3}$;
(2)这三根细木棒能构成直角三角形的概率与这三根细木棒能构成等腰三角形的概率哪一个大?说明理由.
分析 (1)利用完全列举法展示所有9种等可能的结果数,再根据三角形三边的关系找出能构成三角形的结果数,然后根据概率公式求解;
(2)根据勾股定理的逆定理找出能构成直角三角形的结果数,根据等腰三角形的判定找出能构成等腰三角形的结果数,然后根据概率公式计算它们的概率,再比较概率的大小即可.
解答 解:(1)随机取出三根细木棒,共9种等可能的结果数,它们是1、3、3,1、3、4,1、3、5,1、3、4,1、3、5,1、4、5,3、3、4,3、3、5,3、4、5,
其中能构成三角形的结果数为3,所以能构成三角形的概率=$\frac{3}{9}$=$\frac{1}{3}$;
故答案为$\frac{1}{3}$;
(2)这三根细木棒能构成直角三角形的概率=$\frac{1}{9}$,
这三根细木棒能构成等腰三角形的概率=$\frac{3}{9}$=$\frac{1}{3}$,
所以这三根细木棒能构成直角三角形的概率比这三根细木棒能构成等腰三角形的概率小.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了三角形三边的关系、等腰三角形的判定与勾股定理的逆定理.

练习册系列答案
相关题目
13.下列标志中,可以看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.若x1,x2是一元二次方程x2-2x-3=0的两个根,则x1x2的值是( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
 已知抛物线y=ax2-4ax+3和直线y=bx-4b+3相交于一定点A.
已知抛物线y=ax2-4ax+3和直线y=bx-4b+3相交于一定点A.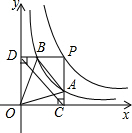 两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是①③④(填序号)
两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是①③④(填序号) 在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.
在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.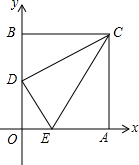 如图,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.
如图,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.