题目内容
16.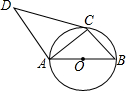 如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.(1)求证:DC与⊙O相切;
(2)若sinB=$\frac{4}{5}$,AB=5,求AD的长.
分析 (1)直接利用圆周角定理得出∠ACB=90°,再利用已知得出DCA+∠ACO=90°,进而求出答案;
(2)利用锐角三角函数关系得出AC的长,再利用勾股定理得出BC的长,再结合相似三角形的判定与性质得出△DAC∽△ACB,则$\frac{AD}{AC}$=$\frac{AC}{BC}$,进而求出答案.
解答 (1)证明:连接CO,
∵AB是⊙O的直径,
∴∠ACB=90°,即∠ACO+∠OCB=90°,
∵CO=OB,
∴∠OCB=∠B,
∵∠DCA=∠B,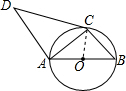
∴∠DCA=∠BCO,
∴DCA+∠ACO=90°,
即∠DCO=90°,
∴DC与⊙O相切;
(2)解:∵sinB=$\frac{4}{5}$,AB=5,
∴$\frac{AC}{AB}$=$\frac{4}{5}$,
∴AC=4,则BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵AD∥BC,
∴∠DAC=∠ACB,
又∵∠DCA=∠B,
∴△DAC∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AC}{BC}$,
即$\frac{AD}{4}$=$\frac{4}{3}$,
解得:AD=$\frac{16}{3}$.
点评 此题主要考查了切线的判定以及相似三角形的判定与性质以及勾股定理、锐角三角函数关系等知识,正确得出△DAC∽△ACB是解题关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
1.已知平行四边形ABCD的周长为32,AB=12,则BC的长为( )
| A. | 4 | B. | 12 | C. | 24 | D. | 28 |
8.在△ABC中,(2cosA-$\sqrt{2}$)2+|1-tanB|=0,则△ABC一定是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
5.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 等腰三角形 | B. | 平行四边形 | C. | 梯形 | D. | 圆 |
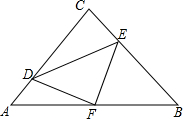 如图,Rt△ABC中,∠ACB=90°,AC=BC=8.D、E是边AC、BC边上的动点,D从A出发向C运动,同时E以相同的速度从C出发向B运动,E运动到B停止.F为AB中点.
如图,Rt△ABC中,∠ACB=90°,AC=BC=8.D、E是边AC、BC边上的动点,D从A出发向C运动,同时E以相同的速度从C出发向B运动,E运动到B停止.F为AB中点.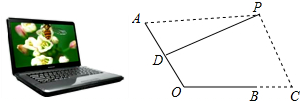
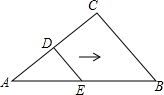 如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为( )
如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为( )