题目内容
8.在△ABC中,(2cosA-$\sqrt{2}$)2+|1-tanB|=0,则△ABC一定是( )| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
分析 根据非负数的和为零,可得每个非负数同时为零,根据特殊角三角函数值,可得A、B的值,根据直角三角形的判定,可得答案.
解答 解:由,(2cosA-$\sqrt{2}$)2+|1-tanB|=0,得
2cosA=$\sqrt{2}$,1-tanB=0.
解得A=45°,B=45°,
则△ABC一定是等腰直角三角形,
故选:D.
点评 本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
19.若$\sqrt{(a-2)^{2}}$=2-a,则a的值( )
| A. | a>2 | B. | a≥2 | C. | a<2 | D. | a≤2 |
3. 如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
 如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 16 |
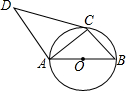 如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.
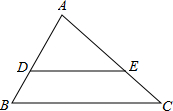 在△ABC中,DE∥BC,若△ADE与△ABC的面积之比1:2,则$\frac{DE}{BC}$=$\frac{\sqrt{2}}{2}$.
在△ABC中,DE∥BC,若△ADE与△ABC的面积之比1:2,则$\frac{DE}{BC}$=$\frac{\sqrt{2}}{2}$.