题目内容
4.如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD⊥AO时,称点P为“最佳视角点”,作PC⊥BC,垂足C在OB的延长线上,且BC=12cm.(1)当PA=45cm时,求PC的长;
(2)若∠AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
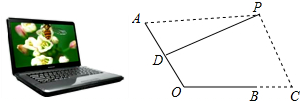
分析 (1)连结PO.先由线段垂直平分线的性质得出PO=PA=45cm,则OC=OB+BC=36cm,然后利用勾股定理即可求出PC=$\sqrt{4{5}^{2}-3{6}^{2}}$=27cm;
(2)过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,则四边形DECF是矩形.先解Rt△DOE,求出DE=DO•sin60°=6$\sqrt{3}$,EO=$\frac{1}{2}$DO=6,则FC=DE=6$\sqrt{3}$,DF=EC=EO+OB+BC=42.再解Rt△PDF,求出PF=DF•tan30°=42×$\frac{\sqrt{3}}{3}$=14$\sqrt{3}$,则PC=PF+FC=14$\sqrt{3}$+6$\sqrt{3}$=20$\sqrt{3}$≈34.68>27,即可得出结论.
解答 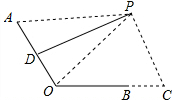 解:(1)当PA=45cm时,连结PO.
解:(1)当PA=45cm时,连结PO.
∵D为AO的中点,PD⊥AO,
∴PO=PA=45cm.
∵BO=24cm,BC=12cm,∠C=90°,
∴OC=OB+BC=36cm,PC=$\sqrt{4{5}^{2}-3{6}^{2}}$=27cm; (2)当∠AOC=120°,过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,则四边形DECF是矩形.
(2)当∠AOC=120°,过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,则四边形DECF是矩形.
在Rt△DOE中,∵∠DOE=60°,DO=$\frac{1}{2}$AO=12,
∴DE=DO•sin60°=6$\sqrt{3}$,EO=$\frac{1}{2}$DO=6,
∴FC=DE=6$\sqrt{3}$,DF=EC=EO+OB+BC=6+24+12=42.
在Rt△PDF中,∵∠PDF=30°,
∴PF=DF•tan30°=42×$\frac{\sqrt{3}}{3}$=14$\sqrt{3}$,
∴PC=PF+FC=14$\sqrt{3}$+6$\sqrt{3}$=20$\sqrt{3}$≈34.68>27,
∴点P在直线PC上的位置上升了.
点评 本题考查了解直角三角形的应用,线段垂直平分线的性质,勾股定理,矩形的判定与性质,锐角三角函数的定义,准确作出辅助线构造直角三角形是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | a>2 | B. | a≥2 | C. | a<2 | D. | a≤2 |
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
 如图,EF⊥AB,CD⊥AB,∠1=∠3,那么DH∥BC吗?为什么?
如图,EF⊥AB,CD⊥AB,∠1=∠3,那么DH∥BC吗?为什么?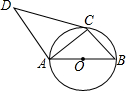 如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.