题目内容
6.学校为了解学生参加体育活动的情况,对学生“平均每天参加体育活动的时间”进行了随机抽样调查,如图是根据调查结果绘制的两幅不完整的统计图.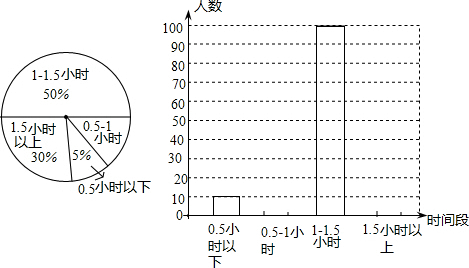
请你根据统计图提供的信息,解答以下问题:
(1)“平均每天参加体育活动的时间”“为0.5~1小时”部分的扇形统计图的圆心角为54度;
(2)本次一共调查了200名学生;
(3)将条形统计图补充完整;
(4)若该校有4000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
分析 (1)先求“0.5~1小时”部分的扇形的百分数,再根据百分数×360°求度数;
(2)根据“1~1.5小时”部分的人数÷对应扇形的百分数,得出调查人数;
(3)根据(1)所求调查人数,各部分对应的百分数,分别求“0.5~1小时”,“1.5小时以上”的人数,补充图形;
(4)根据:该校4000名学生×时间在0.5小时以下的百分数,得出结论.
解答 解:(1)(1-50%-30%-5%)×360°=54°,
(2)100÷50%=200,
(3)(1-50%-30%-5%)×200=30人,30%×200=60人,补充图形如图所示;
(4)4000×5%=200(人).
故答案为:(1)54,(2)200.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
14.已知有9张卡片,分别写有1到9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则使关于x的不等式组$\left\{\begin{array}{l}{4x≥3(x+1)}\\{2x-\frac{x-1}{2}<a}\end{array}\right.$有解的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
15.已知∠α的两边分别与∠β的两边垂直,且∠α=20°,则∠β的度数为( )
| A. | 20° | B. | 160° | C. | 20°或160° | D. | 70° |
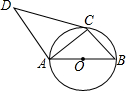 如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.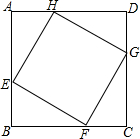 如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH,
如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH,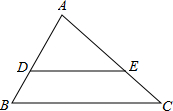 在△ABC中,DE∥BC,若△ADE与△ABC的面积之比1:2,则$\frac{DE}{BC}$=$\frac{\sqrt{2}}{2}$.
在△ABC中,DE∥BC,若△ADE与△ABC的面积之比1:2,则$\frac{DE}{BC}$=$\frac{\sqrt{2}}{2}$.