题目内容
6.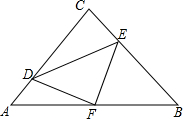 如图,Rt△ABC中,∠ACB=90°,AC=BC=8.D、E是边AC、BC边上的动点,D从A出发向C运动,同时E以相同的速度从C出发向B运动,E运动到B停止.F为AB中点.
如图,Rt△ABC中,∠ACB=90°,AC=BC=8.D、E是边AC、BC边上的动点,D从A出发向C运动,同时E以相同的速度从C出发向B运动,E运动到B停止.F为AB中点.(1)试探究△DEF的形状,并说明理由.
(2)在运动过程中,四边形CDFE可能成为正方形吗?如能求正方形的边长.
(3)当AD为多少时,△DEC的面积最大?最大面积是多少?
分析 (1)根据F是AB中点,可得AF=BF=CF,∠A=∠FCE=45°,即可证明△ADF≌△CEF,于是可得DF=EF,∠AFD=∠CFE,即可求得∠DFE=90°,即可得到结论;
(2)根据三角形中位线定理和等腰直角三角形的性质即可证得;
(3)设AD=x,则CE=x,DC=8-x,根据三角形面积公式得出函数关系式,根据函数的顶点式即可求得.
解答 解:(1)△DEF为等腰直角三角形,
理由:如图连接CF,
∵F是AB中点,AC=BC,∠ACB=90°,
∴AF=BF=CF,∠A=∠FCE=45°,
在△ADF和△CEF中,
$\left\{\begin{array}{l}{AF=CF}\\{∠A=∠FCE=45°}\\{AD=CE}\end{array}\right.$,
∴△ADF≌△CEF(SAS);
∴DF=EF,∠AFD=∠CFE,
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFE=90°,即∠DFE=90°,
∴△DEF是等腰直角三角形;
(2)当D、E分别为AC、BC中点时,四边形CDFE是正方形,
∵∠ACB=90°,F为AB中点,
∴DF=DC=AD=$\frac{1}{2}$AC,EF=EC=$\frac{1}{2}$BC,
∵AC=BC,
∴DC=DF=EF=EC,
又∵∠ACB=90°,
∴四边形CDFE是正方形,且其边长为4;
(3)设AD=x,则CE=x,DC=8-x,
∵S△DEC=$\frac{1}{2}$DC•CE=$\frac{1}{2}$(8-x)•x=-$\frac{1}{2}$x2+4x=-$\frac{1}{2}$(x-4)2+8,
∴当AD为4时,△DEC的面积最大,最大面积是8.
点评 本题考查了全等三角形的性质和判定,等腰三角形性质,等腰直角三角形,二次函数的最值以及正方形的判定,本题中求证△ADF≌△CEF是解题的关键.

 阅读快车系列答案
阅读快车系列答案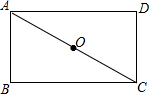 如图,矩形ABCD中,O为AC的中点,△ADC是否可由△CBA旋转得到?若能,请指出旋转中心和旋转角度;若不能,请说明理由.
如图,矩形ABCD中,O为AC的中点,△ADC是否可由△CBA旋转得到?若能,请指出旋转中心和旋转角度;若不能,请说明理由.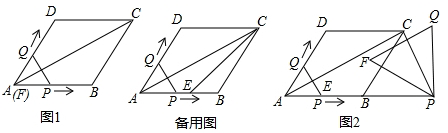
 如图,EF⊥AB,CD⊥AB,∠1=∠3,那么DH∥BC吗?为什么?
如图,EF⊥AB,CD⊥AB,∠1=∠3,那么DH∥BC吗?为什么?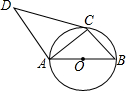 如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.