题目内容
11.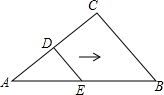 如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为( )
如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据勾股定理得到AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=5,由平行线等分线段定理得到AE=BE=5,根据平移的性质即可得到结论.
解答 解:∵∠C=90°,AD=DC=4,DE=3,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=5,
∵DE∥BC,
∴AE=BE=5,
∴当点D落在BC上时,平移的距离为BE=5.
故选C.
点评 本题考查了平移的性质,平行线等分线段定理,熟记平移的性质是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
2.若a-b=3,ab=1,则a2+b2的值是( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
19.若$\sqrt{(a-2)^{2}}$=2-a,则a的值( )
| A. | a>2 | B. | a≥2 | C. | a<2 | D. | a≤2 |
3. 如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
 如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 16 |
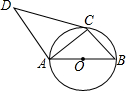 如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B.