题目内容
14. 如图,把⊙O分成相等的6段弧,依次连接各分点得到六边形ABCDEF,求证:六边形ABCDEF是⊙O的内接正六边形.
如图,把⊙O分成相等的6段弧,依次连接各分点得到六边形ABCDEF,求证:六边形ABCDEF是⊙O的内接正六边形.
分析 只要证明6条边相等,6个内角都是120°即可.
解答 解:如图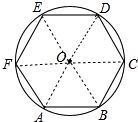 ,连接OA、OB、OC、OD、OE、OF.
,连接OA、OB、OC、OD、OE、OF.
∵$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{EF}$=$\widehat{AF}$,
∴AB=BC=CD=DE=EF=FA,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠FOA=60°,
∵OA=OB=OC=OD=OE=OF,
∴△AOB、△BOC、△DOC、△EOD、△EOF、△AOF都是等边三角形,
∴∠OAB=∠OAF=60°,
∴∠FAB=120°,同理可以证明:∠EFA=∠DEF=∠EDC=∠DCB=∠CBA=120°,
∴六边形ABCDEF是⊙O的内接正六边形.
点评 本题考查正多边形与圆的关系、等边三角形的判定和性质等知识,利用等弧所对的弦相等,所对的圆心角相等是解题的关键,属于中考常考题型.

练习册系列答案
相关题目
3.计算2$\sqrt{3}$+3$\sqrt{\frac{1}{3}}$-3$\sqrt{\frac{1}{27}}$的结果是( )
| A. | $\frac{8}{3}$$\sqrt{3}$ | B. | 8$\sqrt{\frac{1}{3}}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{3}$+$\frac{2}{3}$$\sqrt{\frac{1}{3}}$ |
6.下列同类二次根式合并过程正确的是( )
| A. | 2$\sqrt{3}$-$\sqrt{3}$=2 | B. | a$\sqrt{c}$+b$\sqrt{c}$=a+b$\sqrt{c}$ | C. | 5$\sqrt{a}$+$\frac{1}{2}$$\sqrt{a}$=5+$\frac{1}{2}$$\sqrt{a}$ | D. | $\frac{1}{3}$$\sqrt{3a}$-$\frac{1}{4}$$\sqrt{3a}$=$\frac{1}{12}$$\sqrt{3a}$ |
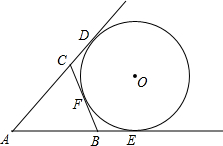 如图,△ABC的周长等于16,圆O与BC相切于点F,AB、AC的延长线与圆分别相切于点E、D,求AE的长.
如图,△ABC的周长等于16,圆O与BC相切于点F,AB、AC的延长线与圆分别相切于点E、D,求AE的长.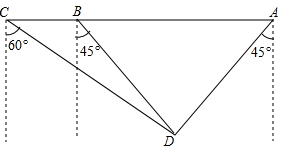 如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,又航行了半小时到达C处,望见渔船D在南偏东60°方向上,若海监船的速度为40海里/时,求A,B之间的距离.(结果保留根号)
如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,又航行了半小时到达C处,望见渔船D在南偏东60°方向上,若海监船的速度为40海里/时,求A,B之间的距离.(结果保留根号)