题目内容
6.抛物线y=-x2+5x+6的顶点A($\frac{5}{2}$,$\frac{49}{4}$),与x轴交点B(-1,0),C(6,0),△ABC的面积为$\frac{343}{8}$.分析 把抛物线化成顶点式,得出顶点坐标;令y=0,求出x的值即可求出点B,C的坐标,求出BC的长,利用S△ABC=$\frac{1}{2}$BC•|A纵坐标|求解即可.
解答 解:∵y=-x2+5x+6=-(x-$\frac{5}{2}$)2+$\frac{49}{4}$,
∴顶点A坐标为($\frac{5}{2}$,$\frac{49}{4}$);
∵y=0,
∴-x2+5x+6=0,
解得:x=-1,或x=6,
∴B(-1,0),C(6,0),
∴BC=OB+OC=7,
∴△ABC的面积=$\frac{1}{2}$×7×$\frac{49}{4}$=$\frac{343}{8}$;
故答案为:($\frac{5}{2}$,$\frac{49}{4}$),(-1,0),(6,0),$\frac{343}{8}$.
点评 本题主要考查了抛物线与x轴的交点及二次函数图象上点的坐标特征,解题的关键是正确求出抛物线与x轴的交点坐标.

练习册系列答案
相关题目
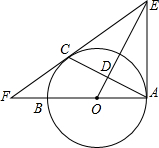 如图,AB为⊙O的直径,C为⊙O上一点,D为AC的中点,过C作⊙O的切线交OD的延长线于E,交AB的延长线于F,连EA.
如图,AB为⊙O的直径,C为⊙O上一点,D为AC的中点,过C作⊙O的切线交OD的延长线于E,交AB的延长线于F,连EA.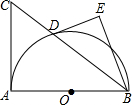 已知,如图,AB是半圆的直径,AC切半圆于A,CB交⊙O于D,DE切⊙O于D,BE⊥DE,垂足是E,BD=10,DE,BE是方程x2-2(m+2)x+2m2-m+3=0的两个根(DE<BE),求AC的长.
已知,如图,AB是半圆的直径,AC切半圆于A,CB交⊙O于D,DE切⊙O于D,BE⊥DE,垂足是E,BD=10,DE,BE是方程x2-2(m+2)x+2m2-m+3=0的两个根(DE<BE),求AC的长. 如图,把⊙O分成相等的6段弧,依次连接各分点得到六边形ABCDEF,求证:六边形ABCDEF是⊙O的内接正六边形.
如图,把⊙O分成相等的6段弧,依次连接各分点得到六边形ABCDEF,求证:六边形ABCDEF是⊙O的内接正六边形.