题目内容
为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
| 污水处理设备 | A型 | B型 |
| 价格(万元/台) | m | m-3 |
| 月处理污水量(吨/台) | 220 | 180 |
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
考点:分式方程的应用,一元一次不等式的应用
专题:应用题
分析:(1)根据90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,列出m的分式方程,求出m的值即可;
(2)设买A型污水处理设备x台,B型则(10-x)台,根据题意列出x的一元一次不等式,求出x的取值范围,进而得出方案的个数,并求出最大值.
(2)设买A型污水处理设备x台,B型则(10-x)台,根据题意列出x的一元一次不等式,求出x的取值范围,进而得出方案的个数,并求出最大值.
解答:解:(1)由90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,
即可得:
=
,
解得m=18,
经检验m=18是原方程的解,即m=18;
(2)设买A型污水处理设备x台,则B型(10-x)台,
根据题意得:18x+15(10-x)≤165,
解得x≤5,由于x是整数,则有6种方案,
当x=0时,10-x=10,月处理污水量为1800吨,
当x=1时,10-x=9,月处理污水量为220+180×9=1840吨,
当x=2时,10-x=8,月处理污水量为220×2+180×8=1880吨,
当x=3时,10-x=7,月处理污水量为220×3+180×7=1920吨,
当x=4时,10-x=6,月处理污水量为220×4+180×6=1960吨,
当x=5时,10-x=5,月处理污水量为220×5+180×5=2000吨,
答:有6种购买方案,每月最多处理污水量的吨数为2000吨.
即可得:
| 90 |
| m |
| 75 |
| m-3 |
解得m=18,
经检验m=18是原方程的解,即m=18;
(2)设买A型污水处理设备x台,则B型(10-x)台,
根据题意得:18x+15(10-x)≤165,
解得x≤5,由于x是整数,则有6种方案,
当x=0时,10-x=10,月处理污水量为1800吨,
当x=1时,10-x=9,月处理污水量为220+180×9=1840吨,
当x=2时,10-x=8,月处理污水量为220×2+180×8=1880吨,
当x=3时,10-x=7,月处理污水量为220×3+180×7=1920吨,
当x=4时,10-x=6,月处理污水量为220×4+180×6=1960吨,
当x=5时,10-x=5,月处理污水量为220×5+180×5=2000吨,
答:有6种购买方案,每月最多处理污水量的吨数为2000吨.
点评:本题考查分式方程的应用和一元一次不等式的应用,分析题意,找到合适的等量关系是解决问题的关键,此题难度不大,特别是几种方案要分析周全.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目


 如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.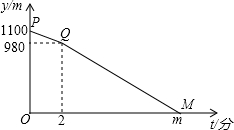 A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象探究:
A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象探究: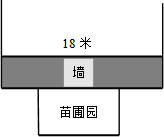 大陇初级中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.如图已知墙长为18米,设这个苗圃园垂直于墙的一边的长为x米.
大陇初级中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.如图已知墙长为18米,设这个苗圃园垂直于墙的一边的长为x米.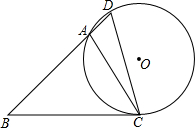 如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3
如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3