题目内容
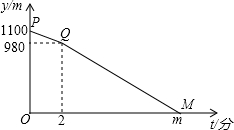 A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象探究:
A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象探究:(1)甲的行进速度为每分钟
(2)求直线PQ对应的函数表达式;
(3)求乙的行进速度.
考点:一次函数的应用
专题:
分析:(1)由函数图象可以求出两分钟行驶的路程就可以求出甲的速度,由相遇时间为7分钟就可以求出m的值;
(2)设直线PQ的解析式为y=kt+b,由待定系数法就可以求出结论;
(3)设乙的行进速度为a米/分,由相遇问题的数量关系建立方程求出其解即可.
(2)设直线PQ的解析式为y=kt+b,由待定系数法就可以求出结论;
(3)设乙的行进速度为a米/分,由相遇问题的数量关系建立方程求出其解即可.
解答:解:(1)由题意,得
甲的行进速度为(1100-980)÷2=60米,m=7+2=9分钟.
故答案为:60,9;
(2)设直线PQ的解析式为y=kt+b,由题意,得
,
解得:
,
y=-60t+1100.
∴直线PQ对应的函数表达式为y=-60t+1100;
(2)设乙的行进速度为a米/分,由题意,得.
980÷(a+60)=7,
解得:a=80.
答:乙的行进速度为80米/分.
甲的行进速度为(1100-980)÷2=60米,m=7+2=9分钟.
故答案为:60,9;
(2)设直线PQ的解析式为y=kt+b,由题意,得
|
解得:
|
y=-60t+1100.
∴直线PQ对应的函数表达式为y=-60t+1100;
(2)设乙的行进速度为a米/分,由题意,得.
980÷(a+60)=7,
解得:a=80.
答:乙的行进速度为80米/分.
点评:本题考查了行程问题的数量关系路程÷时间=速度的运用,待定系数法求一次函数的解析式的运用,解答时认真分析函数图象的数据是关键.

练习册系列答案
相关题目
 如图,P是正方形ABCD内的一点,连结BP、CP,将△PBC绕点B逆时针旋转到△P′BA的位置,则它旋转了
如图,P是正方形ABCD内的一点,连结BP、CP,将△PBC绕点B逆时针旋转到△P′BA的位置,则它旋转了 如图,抛物线y=
如图,抛物线y=
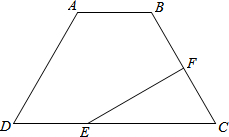 已知:如图,梯形ABCD中,AD=BC,F为BC的中点,AB=2,∠A=120°,过点F作EF⊥BC交DC于点E,且EF=3,求DC的长.
已知:如图,梯形ABCD中,AD=BC,F为BC的中点,AB=2,∠A=120°,过点F作EF⊥BC交DC于点E,且EF=3,求DC的长. 如图,一次函数y=kx+2的图象与反比例函数
如图,一次函数y=kx+2的图象与反比例函数