题目内容
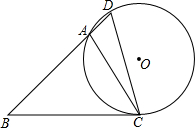 如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3
如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3| 2 |
(1)求BC的长;
(2)求⊙O的半径.
考点:三角形的外接圆与外心,圆周角定理,解直角三角形
专题:
分析:(1)根据题意得出AE的长,进而得出BE=AE,再利用tan∠ACB=
,求出EC的长即可;
(2)首先得出AC的长,再利用圆周角定理得出∠D=∠M=60°,进而求出AM的长,即可得出答案.
| AE |
| EC |
(2)首先得出AC的长,再利用圆周角定理得出∠D=∠M=60°,进而求出AM的长,即可得出答案.
解答: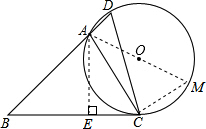 解:(1)过点A作AE⊥BC,垂足为E,
解:(1)过点A作AE⊥BC,垂足为E,
∴∠AEB=∠AEC=90°,
在Rt△ABE中,∵sinB=
,
∴AE=ABsinB=3
sin45°=3
×
=3,
∵∠B=45°,
∴∠BAE=45°,
∴BE=AE=3,
在Rt△ACE中,
∵tan∠ACB=
,
∴EC=
=
=
=
,
∴BC=BE+EC=3+
;
(2)连接AO并延长到⊙O上一点M,连接CM,
由(1)得,在Rt△ACE中,∵∠EAC=30°,EC=
,
∴AC=2
,
∵∠D=∠M=60°,
∴sin60°=
=
=
,
解得:AM=4,
∴⊙O的半径为2.
 解:(1)过点A作AE⊥BC,垂足为E,
解:(1)过点A作AE⊥BC,垂足为E,∴∠AEB=∠AEC=90°,
在Rt△ABE中,∵sinB=
| AE |
| AB |
∴AE=ABsinB=3
| 2 |
| 2 |
| ||
| 2 |
∵∠B=45°,
∴∠BAE=45°,
∴BE=AE=3,
在Rt△ACE中,
∵tan∠ACB=
| AE |
| EC |
∴EC=
| AE |
| tan∠ACB |
| 3 |
| tan60° |
| 3 | ||
|
| 3 |
∴BC=BE+EC=3+
| 3 |
(2)连接AO并延长到⊙O上一点M,连接CM,
由(1)得,在Rt△ACE中,∵∠EAC=30°,EC=
| 3 |
∴AC=2
| 3 |
∵∠D=∠M=60°,
∴sin60°=
| AC |
| AM |
2
| ||
| AM |
| ||
| 2 |
解得:AM=4,
∴⊙O的半径为2.
点评:此题主要考查了解直角三角形以及锐角三角函数关系应用,根据题意正确构造直角三角形是解题关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
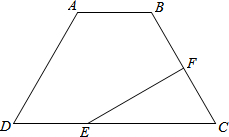 已知:如图,梯形ABCD中,AD=BC,F为BC的中点,AB=2,∠A=120°,过点F作EF⊥BC交DC于点E,且EF=3,求DC的长.
已知:如图,梯形ABCD中,AD=BC,F为BC的中点,AB=2,∠A=120°,过点F作EF⊥BC交DC于点E,且EF=3,求DC的长. 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′. 如图,一次函数y=kx+2的图象与反比例函数
如图,一次函数y=kx+2的图象与反比例函数 如图,AD是△ABC的一条中线,若BD=5,则BC=
如图,AD是△ABC的一条中线,若BD=5,则BC= 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=