题目内容
【探究】如图1,在△ABC中,D是AB边的中点,AE⊥BC于点E,BF⊥AC于点F,AE,BF相交于点M,连接DE,DF.则DE,DF的数量关系为 .
【拓展】如图2,在△ABC中,CB=CA,点D是AB边的中点,点M在△ABC的内部,且∠MBC=∠MAC.过点M作ME⊥BC于点E,MF⊥AC于点F,连接DE,DF.求证:DE=DF;
【推广】如图3,若将上面【拓展】中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.

【拓展】如图2,在△ABC中,CB=CA,点D是AB边的中点,点M在△ABC的内部,且∠MBC=∠MAC.过点M作ME⊥BC于点E,MF⊥AC于点F,连接DE,DF.求证:DE=DF;
【推广】如图3,若将上面【拓展】中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.

考点:全等三角形的判定与性质,直角三角形斜边上的中线,三角形中位线定理
专题:
分析:探究:依据直角三角形斜边上的中线等于斜边的一半即可求得.
拓展:连接CD,可证得CD是角ACD的平分线,根据△CMF≌△CME可求得CF=CE,从而求得AF=BE,然后再证得△CFD≌△CED即可求得.
推广:作△ABM的中位线DG、DF,可得DH=FG,DG=HE,四边形DHMG是平行四边形,根据已知和平行四边形求得∠DGF=∠DHE,求得△DHE≌△FGD,从而求得结论.
拓展:连接CD,可证得CD是角ACD的平分线,根据△CMF≌△CME可求得CF=CE,从而求得AF=BE,然后再证得△CFD≌△CED即可求得.
推广:作△ABM的中位线DG、DF,可得DH=FG,DG=HE,四边形DHMG是平行四边形,根据已知和平行四边形求得∠DGF=∠DHE,求得△DHE≌△FGD,从而求得结论.
解答:解:【探究】DE=DF.
【拓展】如图2,连接CD.
∵在△A B C中,C B=C A,
∴∠CAB=∠CBA.
∵∠MBC=∠MAC,
∴∠MAB=∠MBA,
∴AM=BM.
∵点 D是 边 AB的 中点,
∴点M在CD上,
∴CM平分∠FCE.
∴∠FCD=∠ECD.
∵ME⊥BC于E,MF⊥AC于F,
∴MF=ME.
在△CMF和△CME中,
∴△CMF≌△CME(SAS).
∴CF=CE.
在△CFD与△CED中
∴△CFD≌△CED(SAS).
∴DE=DF,
【推广】DE=DF.
如图3,作AM的中点G,BM的中点H.
∵点 D是 边 AB的 中点,
∴DG∥BM,DG=
BM.
同理可得:DH∥AM,DH=
AM.
∵ME⊥BC于E,H 是BM的中点,
∴在Rt△BEM中,HE=
BM=BH.
∴DG=HE,
同理可得:DH=FG.
∵DG∥BM,DH∥GM,
∴四边形DHMG是平行四边形.
∴∠DGM=∠DHM.
∵∠MGF=2∠MAC,∠MHE=2∠MBC,
又∵∠MBC=∠MAC,
∴∠MGF=∠MHE.
∴∠DGM+∠MGF=∠DHM+∠MHE.
∴∠DGF=∠DHE,
在△DHE与△FGD中,
∴△DHE≌△FGD(SAS),
∴DE=DF.
【拓展】如图2,连接CD.
∵在△A B C中,C B=C A,
∴∠CAB=∠CBA.
∵∠MBC=∠MAC,

∴∠MAB=∠MBA,
∴AM=BM.
∵点 D是 边 AB的 中点,
∴点M在CD上,
∴CM平分∠FCE.
∴∠FCD=∠ECD.
∵ME⊥BC于E,MF⊥AC于F,
∴MF=ME.
在△CMF和△CME中,
|
∴△CMF≌△CME(SAS).
∴CF=CE.
在△CFD与△CED中
|
∴△CFD≌△CED(SAS).
∴DE=DF,
【推广】DE=DF.
如图3,作AM的中点G,BM的中点H.
∵点 D是 边 AB的 中点,
∴DG∥BM,DG=
| 1 |
| 2 |

同理可得:DH∥AM,DH=
| 1 |
| 2 |
∵ME⊥BC于E,H 是BM的中点,
∴在Rt△BEM中,HE=
| 1 |
| 2 |
∴DG=HE,
同理可得:DH=FG.
∵DG∥BM,DH∥GM,
∴四边形DHMG是平行四边形.
∴∠DGM=∠DHM.
∵∠MGF=2∠MAC,∠MHE=2∠MBC,
又∵∠MBC=∠MAC,
∴∠MGF=∠MHE.
∴∠DGM+∠MGF=∠DHM+∠MHE.
∴∠DGF=∠DHE,
在△DHE与△FGD中,
|
∴△DHE≌△FGD(SAS),
∴DE=DF.
点评:本题考查了直角三角形的性质的运用,等腰三角形的性质的运用,全等三角形的判定及性质的运用,三角形的中位线的性质的运用,直角三角形的斜边上的中线的性质的运用,平行四边形性质的运用,解答时根据三角形的中位线的性质制造全等三角形是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某校将举办一场“中国汉字听写大赛”,要求各班推选一名同学参加比赛,为此,初三(1)班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是96分,甲的成绩的方差是0.2,乙的成绩的方差是0.8.根据以上数据,下列说法正确的是( )
| A、甲的成绩比乙的成绩稳定 |
| B、乙的成绩比甲的成绩稳定 |
| C、甲、乙两人的成绩一样稳定 |
| D、无法确定甲、乙的成绩谁更稳定 |
“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1-(x-a)(x-b)=0的两根,且a<b,则a、b、m、n的大小关系是( )
| A、m<a<b<n |
| B、a<m<n<b |
| C、a<m<b<n |
| D、m<a<n<b |
 如图,P是正方形ABCD内的一点,连结BP、CP,将△PBC绕点B逆时针旋转到△P′BA的位置,则它旋转了
如图,P是正方形ABCD内的一点,连结BP、CP,将△PBC绕点B逆时针旋转到△P′BA的位置,则它旋转了 如图,抛物线y=
如图,抛物线y=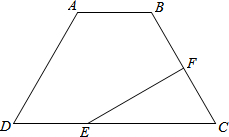 已知:如图,梯形ABCD中,AD=BC,F为BC的中点,AB=2,∠A=120°,过点F作EF⊥BC交DC于点E,且EF=3,求DC的长.
已知:如图,梯形ABCD中,AD=BC,F为BC的中点,AB=2,∠A=120°,过点F作EF⊥BC交DC于点E,且EF=3,求DC的长.