题目内容
9．若矩形的一条对角线与一边的夹角是40°，则两条对角线所夹的锐角的度数为（ ）| A． | 80° | B． | 60° | C． | 45° | D． | 40° |
分析 根据矩形的性质，得△BOC是等腰三角形，再由等腰三角形的性质进行答题．
解答 解：图形中∠1=40°，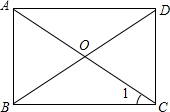
∵矩形的性质对角线相等且互相平分，
∴OB=OC，
∴△BOC是等腰三角形，
∴∠OBC=∠1，则∠AOB=2∠1=80°．
故选A．
点评 本题主要考查了矩形的性质，能运用矩形的性质进行推理和计算是解此题的关键，注意：矩形的对角线相等且互相平分，矩形被对角线分成四个等腰三角形．
练习册系列答案
相关题目
14．下列说法正确的是（ ）
| A． | 有且只有一条直线与已知直线平行 | |
| B． | 垂直于同一条直线的两条直线互相平行 | |
| C． | 从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离 | |
| D． | 在平面内过一点有且只有一条直线与已知直线垂直 |
1．
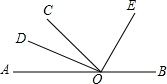∠AOC与∠BOC是邻补角，OD、OE分别是∠AOC与∠BOC的平分线，试判断OD与OE的夹角为（ ）度．
∠AOC与∠BOC是邻补角，OD、OE分别是∠AOC与∠BOC的平分线，试判断OD与OE的夹角为（ ）度．| A． | 60° | B． | 65° | C． | 90° | D． | 80° |
18．如果用总长为60m的篱笆围成一个长方形场地，设长方形的面积为S（m2），周长为p（m），一边长为a（m），那么S，p，a中是变量的是（ ）
| A． | S和p | B． | S和a | C． | p和a | D． | S，p，a |
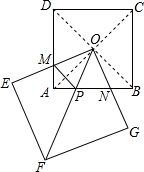如图，正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转，边OE、OG分别交边AD、AB于点M、N．