题目内容
19.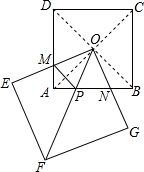 如图,正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.
如图,正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.(1)求证:OM=ON;
(2)设正方形OEFG的对角线OF与边AB相交于点P,连结PM.若PM=13,试求AM的长;
(3)连接MN,求△AMN周长的最小值,并指出此时线段MN与线段BD的关系.
分析 (1)首先判断出∠OAM=∠OBN,∠AOM=∠BON,然后根据全等三角形的判定方法,判断出△AOM≌△BON,即可判断出OM=ON.
(2)首先根据全等三角形的判定方法,判断出△POM≌△PON,PN=PM=5;然后根据△AOM≌△BON,判断出BN=AM;最后在Rt△AMP中,根据AM2+AP2=PM2,求出AM的长是多少即可.
(3)首先根据在Rt△AMN中,AM2+AN2=MN2,判断出当x=15时,即AM=15时,线段MN的长度最小,并求出此时MN、AN的值,求出△AMN周长的最小值是多少;然后判断出MN是△ABD的中位线,即可判断出MN∥BD,且MN=$\frac{1}{2}BD$.
解答 (1)证明:在正方形ABCD中,∠OAM=∠OBN=45°,OA=OB,
∵∠AOM+∠AON=∠EOG=90°,∠BON+∠AON=∠AOB=90°,
∴∠AOM=∠BON,
在△AOM和△BON中,
$\left\{\begin{array}{l}{∠OAM=∠OBN}\\{OA=OB}\\{∠AOM=∠BON}\end{array}\right.$
∴△AOM≌△BON,
∴OM=ON.
(2)解:∵OF是正方形OEFG的对角线,
∴∠POM=∠PON,
在△POM和△PON中,
$\left\{\begin{array}{l}{OM=ON}\\{∠POM=∠PON}\\{OP=OP}\end{array}\right.$
∴△POM≌△PON,
∴PN=PM=13,
∵△AOM≌△BON,
∴BN=AM,
设AM=BN=x,
则AP=AB-BN-PN=30-x-13=17-x,
在Rt△AMP中,
AM2+AP2=PM2,
即x2+(17-x)2=132,
解得x1=5,x2=12,
所以AM的长为5或12.
(3)设AM=BN=x,
则AN=AB-BN=30-x,
在Rt△AMN中,
AM2+AN2=MN2,
即MN2=x2+(30-x)2=2(x-15)2+450
∴当x=15时,即AM=15时,线段MN的长度最小,
此时MN=$\sqrt{450}=15\sqrt{2}$,
AN=30-x=30-15$\sqrt{2}$,
∴△AMN周长的最小值是30+15$\sqrt{2}$.
∵点M是AD的中点,点N是AB的中点,
∴MN是△ABD的中位线,
∴MN∥BD,且MN=$\frac{1}{2}BD$.
点评 (1)此题主要考查了几何变换综合题,以及线段的最大值、最小值的求解,考查了分析推理能力,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握.
(3)此题还考查了直角三角形的性质和应用,以及三角形的中位线的性质和应用,要熟练掌握.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案| A. | 80° | B. | 60° | C. | 45° | D. | 40° |
| A. | 35°12′ | B. | 35°48′ | C. | 55°12′ | D. | 55°48′ |
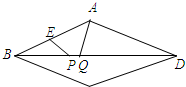 如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )
如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )| A. | 16 | B. | 21 | C. | 7+$\sqrt{85}$ | D. | 7+$\sqrt{61}$ |
| A. | y=2x | B. | y=$\frac{2}{x}$ | C. | y=$\frac{2}{x+1}$ | D. | y=$\frac{2}{{x}^{2}}$ |
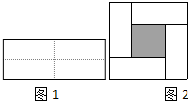 把一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1)
把一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1)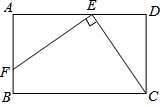 如图,在矩形ABCD中,EF⊥CE,EF=CE,DE=2cm,矩形的周长为32cm,求矩形ABCD的面积.
如图,在矩形ABCD中,EF⊥CE,EF=CE,DE=2cm,矩形的周长为32cm,求矩形ABCD的面积.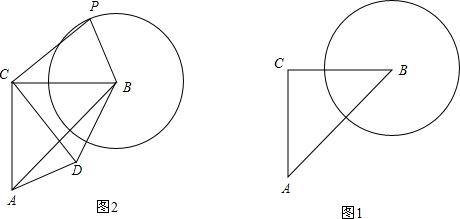
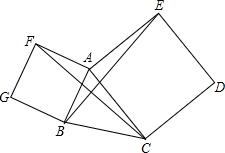 已知,如图,分别以△ABC的边AC,AB为边的三角形作正方形ACDE、BAFG.
已知,如图,分别以△ABC的边AC,AB为边的三角形作正方形ACDE、BAFG.