题目内容
1.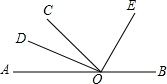 ∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.| A. | 60° | B. | 65° | C. | 90° | D. | 80° |
分析 根据角平分线可得∠COD=$\frac{1}{2}$∠AOC,∠COE=$\frac{1}{2}$∠BOC,根据互为邻补角的定义,可求出∠DOE=90°.
解答 解:∵OD是∠AOC的平分线,
∴∠COD=$\frac{1}{2}$∠AOC,
∵OE是∠BOC的平分线,
∴∠COE=$\frac{1}{2}$∠BOC.
∵∠AOC+∠BOC=180°,
∴∠COD+∠COE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=90°,
∴∠DOE=90°.
故选:C.
点评 此题主要考查了角平分线和邻补角的性质,解题关键是角平分线定义及邻补角互补.

练习册系列答案
相关题目
9.若矩形的一条对角线与一边的夹角是40°,则两条对角线所夹的锐角的度数为( )
| A. | 80° | B. | 60° | C. | 45° | D. | 40° |
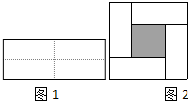 把一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1)
把一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1)