题目内容
13.已知:a2+b2-2a+4b+5=0,c是(2+1)(22+1)(24+1)…(232+1)+1的个位数字,求(a+c)b的值.分析 先利用平方分得出a、b的数值,再把2+1变成22-1,然后逐个使用平方差公式,算出结果,再根据2的整数次幂的个位数字的规律,可判断最后结果的个位数字得出c,进一步代入求得答案即可.
解答 解:∵a2+b2-2a+4b+5=0,
∴(a-1)2+(b+2)2=0,
∴a=1,b=-2,
∵(2+1)(22+1)(24+1)…(232+1)+1
=(22-1)(22+1)(24+1)(28+1)…(232+1)+1
=(24-1)(24+1)(28+1)…(232+1)+1
=264-1+1
=264;
∵21=2,22=4,23=8,24=16,25=32,…
∴2的整数次幂的个位数字每4个数字为一个循环组依次循环,
∵64=16×4,
∴264的个位数字与24的个位数字相同,为6,
∴原式的个位数字为6,即c=6;
∴(a+c)b=$\frac{1}{49}$.
点评 此题考查配方法的实际运用,非负数的性质,乘方的尾数特征,掌握完全平方公式和平方差公式是解决问题的关键.

练习册系列答案
相关题目
3.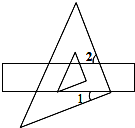 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=25°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=25°,则∠2的度数为( )
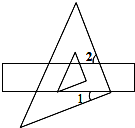 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=25°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=25°,则∠2的度数为( )| A. | 25° | B. | 65° | C. | 55° | D. | 40° |
3. 如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )
如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )
 如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )
如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
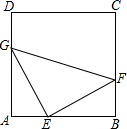 如图,正方形ABCD中,点E,F,G分别为边AB,BC,AD上的点,且AE=BF=DG,连接EF,GE,GF.
如图,正方形ABCD中,点E,F,G分别为边AB,BC,AD上的点,且AE=BF=DG,连接EF,GE,GF. 如图,AC丄BC,AC=9cm,BC=12cm,AB=15cm,点C到直线AB的距离是为$\frac{36}{5}$cm.
如图,AC丄BC,AC=9cm,BC=12cm,AB=15cm,点C到直线AB的距离是为$\frac{36}{5}$cm.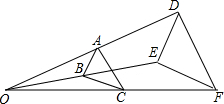 如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的$\frac{1}{4}$,则$\frac{AB}{DE}$=$\frac{1}{2}$.
如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的$\frac{1}{4}$,则$\frac{AB}{DE}$=$\frac{1}{2}$.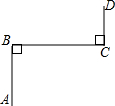 如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是AB∥CD.
如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是AB∥CD.