题目内容
2.解不等式组:$\left\{\begin{array}{l}{4x+6>1-x}\\{3(x-1)≤x+5}\end{array}\right.$,并把解集在数轴上表示出来.分析 别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:$\left\{\begin{array}{l}{4x+6>1-x①}\\{3(x-1)≤x+5②}\end{array}\right.$,
由①得,x>-1;
由②得,x≤4,
故此不等式组的解集为:-1<x≤4,
在数轴上表示为:
点评 本题考查的是解一元一次不等式组,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
相关题目
10.计算$(-\frac{5}{13}{)^3}$×$(-\frac{13}{5}{)^2}$所得结果为( )
| A. | 1 | B. | -1 | C. | $-\frac{5}{13}$ | D. | $-\frac{13}{5}$ |
12.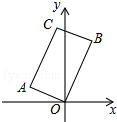 如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
 如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{7}{4}$,$\frac{7}{2}$)、(-$\frac{1}{2}$,4) | B. | ($\frac{3}{2}$,3)、(-$\frac{2}{3}$,4) | C. | ($\frac{3}{2}$,3)、(-$\frac{1}{2}$,4) | D. | ($\frac{7}{4}$,$\frac{7}{2}$)、(-$\frac{2}{3}$,4) |
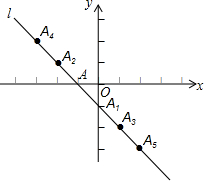 如图在平面直角坐标系xOy中,直线l经过点 A(-1,0),点 A1,A2,A3,A4,A5,…按所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n=4031.
如图在平面直角坐标系xOy中,直线l经过点 A(-1,0),点 A1,A2,A3,A4,A5,…按所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n=4031. 北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=3米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=3米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)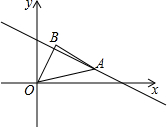 如图,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点;连接OA,以OA为斜边向上作等腰直角三角形OAB,若点A的横坐标为4,则点B的坐标为($\frac{3}{2}$,$\frac{5}{2}$).
如图,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点;连接OA,以OA为斜边向上作等腰直角三角形OAB,若点A的横坐标为4,则点B的坐标为($\frac{3}{2}$,$\frac{5}{2}$).