题目内容
18．
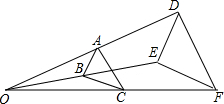如图，△ABC与△DEF位似，位似中心为点O，且△ABC的面积等于△DEF面积的$\frac{1}{4}$，则$\frac{AB}{DE}$=$\frac{1}{2}$．
分析 由△ABC与△DEF位似，位似中心为点O，且△ABC的面积等于△DEF面积的$\frac{1}{4}$，根据相似三角形的面积比等于相似比的平方，即可求得答案．
解答 解：∵△ABC与△DEF位似，位似中心为点O，且△ABC的面积等于△DEF面积的$\frac{1}{4}$，
∴△ABC与△DEF位似的位似比为：$\frac{1}{2}$，
即$\frac{AB}{DE}$=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 此题考查了位似图形的性质．注意位似是特殊的相似，相似三角形的面积比等于相似比的平方．
练习册系列答案
步步高达标卷系列答案
相关题目
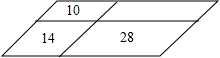农业技术员在一块平行四边形的实验田里种植四种不同的农作物，现需将该实验田划成四个平行四边形地块（如图），已知其中三块田的面积分别是14m2，10m2，28m2，则第四块田的面积为20m2．
将平行四边形纸片ABCD按如图方式折叠，使点C与点A重合，点D落到D′处，折痕为EF．
10．计算$（-\frac{5}{13}{）^3}$×$（-\frac{13}{5}{）^2}$所得结果为（ ）
| A． | 1 | B． | -1 | C． | $-\frac{5}{13}$ | D． | $-\frac{13}{5}$ |
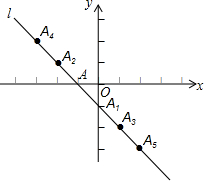如图在平面直角坐标系xOy中，直线l经过点 A（-1，0），点 A1，A2，A3，A4，A5，…按所示的规律排列在直线l上．若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1，若点An（n为正整数）的横坐标为2015，则n=4031．