题目内容
1.有如下命题:①在平面直角坐标系中,水平方向的数轴为x轴或横轴,竖直方向的数轴称为y轴或纵轴;
②x轴上所有点的纵坐标都等于0;
③点M(0,1)在坐标平面内的位置时第三象限或第四象限;
④平行于x轴的点的横坐标都相同.
其中正确的个数有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 直接利用平面直角坐标系的构成以及象限内点的特点分析得出答案.
解答 解:①在平面直角坐标系中,水平方向的数轴为x轴或横轴,竖直方向的数轴称为y轴或纵轴,正确;
②x轴上所有点的纵坐标都等于0,正确;
③点M(0,1)在y轴上,故原命题错误;
④平行于x轴的点的纵坐标都相同,故原命题错误.
故选:B.
点评 此题主要考查了命题与定理,正确掌握平面直角坐标系中点的坐标特点是解题关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
11.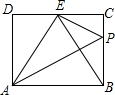 如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )
如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )
 如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )
如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
16.下列说法:
(1)正数和负数统称有理数;
(2)相反数大于本身的数是负数;
(3)(-1)2n+(-1)2n-1=1(n是正整数);
(4)若|a|=|b|,则a=b.
其中正确的个数有( )
(1)正数和负数统称有理数;
(2)相反数大于本身的数是负数;
(3)(-1)2n+(-1)2n-1=1(n是正整数);
(4)若|a|=|b|,则a=b.
其中正确的个数有( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
10.计算$(-\frac{5}{13}{)^3}$×$(-\frac{13}{5}{)^2}$所得结果为( )
| A. | 1 | B. | -1 | C. | $-\frac{5}{13}$ | D. | $-\frac{13}{5}$ |
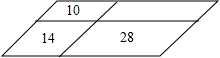 农业技术员在一块平行四边形的实验田里种植四种不同的农作物,现需将该实验田划成四个平行四边形地块(如图),已知其中三块田的面积分别是14m2,10m2,28m2,则第四块田的面积为20m2.
农业技术员在一块平行四边形的实验田里种植四种不同的农作物,现需将该实验田划成四个平行四边形地块(如图),已知其中三块田的面积分别是14m2,10m2,28m2,则第四块田的面积为20m2.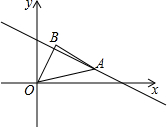 如图,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点;连接OA,以OA为斜边向上作等腰直角三角形OAB,若点A的横坐标为4,则点B的坐标为($\frac{3}{2}$,$\frac{5}{2}$).
如图,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点;连接OA,以OA为斜边向上作等腰直角三角形OAB,若点A的横坐标为4,则点B的坐标为($\frac{3}{2}$,$\frac{5}{2}$).