题目内容
12.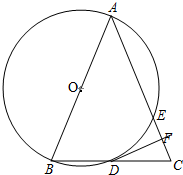 如图,AB为⊙O的直径,点D为⊙O上的一点,在BD的延长线上取点C,使DC=BD,AC与⊙O交于点E,DF⊥AC于点F.求证:
如图,AB为⊙O的直径,点D为⊙O上的一点,在BD的延长线上取点C,使DC=BD,AC与⊙O交于点E,DF⊥AC于点F.求证:(1)DF是⊙O的切线;
(2)DB2=CF•AB.
分析 (1)根据三角形中位线定理得到OD∥AC,根据平行线的性质得到DF⊥OD,根据切线的判定定理证明即可;
(2)证明△CDF∽△CAD,根据相似三角形的性质定理证明即可.
解答 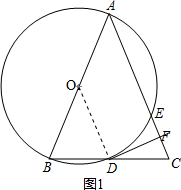 证明(1)如图1,连接OD,
证明(1)如图1,连接OD,
∵OA=OB,BD=DC,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)如图2,连接AD,
∵AB为⊙O的直径,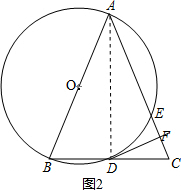 ∴∠ADB=∠ADC=90°,
∴∠ADB=∠ADC=90°,
∴AD⊥BC,
又∵BD=DC,
∴AB=AC,
∵DF⊥AC,
∴∠DFC=90°,
∴∠DFC=∠ADC=90°,
又∵∠C=∠C,
∴△CDF∽△CAD,
∴$\frac{CD}{CF}=\frac{AC}{CD}$,即:CD2=CF•AC.
又∵BD=CD,AB=AC,
∴DB2=CF•AB.
点评 本题考查的是切线的判定定理、等腰三角形的判定和性质定理以及相似三角形的判定和性质定理,灵活运用相关的定理、正确作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
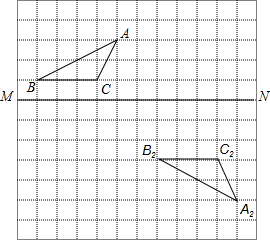 在如图所示的方格纸中.
在如图所示的方格纸中. 如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠ADE的度数为60°.
如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠ADE的度数为60°.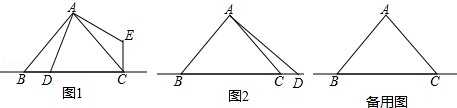
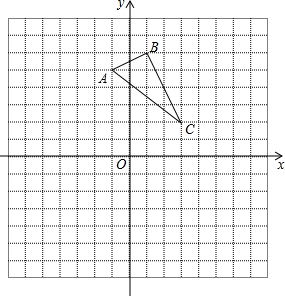 已知如图,在平面直角坐标系xOy中,A(-1,5),B(1,6),C(3,2),请在图中作出△ABC关于x轴的轴对称图形△A1B1C1.
已知如图,在平面直角坐标系xOy中,A(-1,5),B(1,6),C(3,2),请在图中作出△ABC关于x轴的轴对称图形△A1B1C1.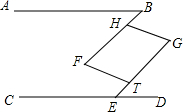 如图,已知AB∥CD,∠B=∠GED,∠F=∠G,试判断BF与GE有怎样的位置关系?HG与FT呢?请说明理由.
如图,已知AB∥CD,∠B=∠GED,∠F=∠G,试判断BF与GE有怎样的位置关系?HG与FT呢?请说明理由.