题目内容
2.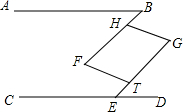 如图,已知AB∥CD,∠B=∠GED,∠F=∠G,试判断BF与GE有怎样的位置关系?HG与FT呢?请说明理由.
如图,已知AB∥CD,∠B=∠GED,∠F=∠G,试判断BF与GE有怎样的位置关系?HG与FT呢?请说明理由.
分析 延长BF交CD于点K,根据平行线的性质可得出∠B=∠EKF,再由∠B=∠GED可得出∠EKF=∠GED,故可得出BF∥GE.由平行线的性质得出∠HFT=∠FTE,故可得出∠FTE=∠G,进而可得出HG∥FT.
解答 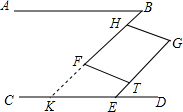 解:BF∥GE,HG∥FT.
解:BF∥GE,HG∥FT.
理由:延长BF交CD于点K,
∵AB∥CD,
∴∠B=∠EKF.
∵∠B=∠GED,
∴∠EKF=∠GED,
∴BF∥GE,
∴∠HFT=∠FTE,
∵∠F=∠G,
∴∠FTE=∠G,
∴HG∥FT.
点评 本题考查的是平行线的判定定理,根据题意作出辅助线,构造出内错角是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.近三年来,我县职业中专的基础设施建设大幅度提升,实调设备购置累计资金1005.69万元,总值达到了2009万元,在校生规模达到3240余人.9个专业中,6个专业达到了规范化专业标准,将3240用科学记数法表示为( )
| A. | 324×101 | B. | 3.24×104 | C. | 3.24×103 | D. | 32.4×102 |
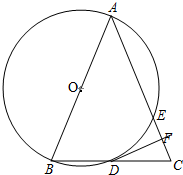 如图,AB为⊙O的直径,点D为⊙O上的一点,在BD的延长线上取点C,使DC=BD,AC与⊙O交于点E,DF⊥AC于点F.求证:
如图,AB为⊙O的直径,点D为⊙O上的一点,在BD的延长线上取点C,使DC=BD,AC与⊙O交于点E,DF⊥AC于点F.求证: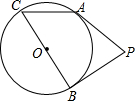 如图,点P在⊙O外,PA、PB是⊙O的切线,A、B是切点,BC是直径,若∠APB=70°,则∠ACB的度数为55°.
如图,点P在⊙O外,PA、PB是⊙O的切线,A、B是切点,BC是直径,若∠APB=70°,则∠ACB的度数为55°.